Preventing Posterior Collapse With Delta-VAEs
by Taemin Kim
Preventing Posterior Collapse With Delta-VAEs
Ali Razavi, Aaron van den Oord, Ben Poole, Oriol Vinyals [ICLR 2019]
Contents
(Contents의 순서는 논문의 순서를 따름)
- Background
- Posterior Collapse
- Introduction
- Mitigating Posterior Collapse with δ-VAEs
- δ-VAE with Sequential Latent Variables
- Anti-Causal Encoder Network
- Experiments
- Natural Images
- Utilization of Latent Variables
- Ablation Studies
- Conclusions
-
Future Work
0. Background
-
- Posterior Collapse란?
- Posterior Collapse는 Variational Auto Encoder(VAE)에서 주요한 문제 중 하나다. variational distribution이 prior distribution과 거의 유사해 지면서 decoder가 encoder에서 나온 latent variable에 대한 정보를 사용하지 못하게 되고, 따라서 VAE의 sample generate 능력을 감소시키게 되는 문제이다.
(James Lucas, George Tucker, Roger Grosse, Mohammad Norouzi, “Don’t Blame the ELBO! A Linear VAE Perspective on Posterior Collapse” NeurIPS 2019.)
-
1. Amortized Variational Inference
-
- Amortized Variational Inference란?
-
우선 Amortized라는 말은 수행된 모든 연산에 대해 필요한 시간의 평균을 이용한다는 말이다. 어떤 시퀀스를 수행할 때 하나의 연산이 너무 비싸더라도(expensive), 그 일련의 연산에 대해 평균을 구하면 연산 하나의 평균 비용이 작다는 것을 알 수 있다. 즉, 데이터를 활용한 분석이라고 할 수 있다. 그렇다면 Amortized Variational Inference는 어떤 Distribution을 데이터를 이용하여 추론함을 의미하며, 데이터(evidence)를 input으로 하는 Neural Net으로 학습하여 inference 수식을 추론하는 것이다. 예를 들어 만약 distribution이 normal이라고 가정하면, data를 input으로 입력하여 mean, variance를 추론하게 된다.
1. Introduction
-
- Prior Work
- Autoregressive Model과 Representation Learning의 장단점은 아래와 같다
- Autoregressive Model
장점 - 지역적인(local) 정보를 얻는데 용이하다.
단점 - 전체적인(global) 구조를 파악하는데 어려움이 있다. - Representation Learning
장접 - 전체적인(global) 구조를 파악이 용이하다.
단점 - 복잡하고 지역적인(local) 구조를 파악하는데 어려움이 있다.
따라서 이 두가지 모델을 조합하여 장점을 극대화 하는 연구들이 많이 진행되었고, 좋은 결과(High quality)를 만들어내고 있다. 하지만 강력한 Autoregressive Decoder를 사용하게 되면, generating 과정에서 Encoder에서 생성된 Latent Variable들이 무시되는 Posterior Collapse 현상이 발생하게 된다. 일반적으로 Posterior Collapse를 해결하기 위해 일반적으로 아래 두 가지 방법이 많이 연구되었다.
1) Objective를 개선하는 방법 2) 약한 Decoder를 사용하는 방법 -
- Proposed Work
-
본 논문은 위에 언급한, Posterior Collapse를 해결하기 위한 일반적인 방법을 사용하지 않고(즉, 강력한 Decoder를 사용하고 Objective를 바꾸지 않으면서) Posterior Collapse를 개선하는 방법을 제안한다.
2. Mitigating Posterior Collapse with δ-VAEs
#### * δ-VAE
- VAE의 Training 과정은 ELBO를 최대화 하는 것이다. Kingma & Welling, 2013
ELBO는 아래와 같이 표현된다.
-
Posterior Collapse는 KL Divergence term에 의해서 발생한다고 알려져 있다. approximate posterior인 q(z x)가 prior인 p(z)와 동일해 지면 KL Divergence term이 0으로 수렴하게 되고, generate할 때 Latent Variable은 input x에 대한 아무런 정보를 전달할 수 없게 되는 것이다. - δ-VAE는 KL Dievergence가 0이 되지 않도록 lower bound δ를 설정해 주는 것이다. 논문에서는 δ를 committed rate라고 부른다. 따라서 KL Divergece는 아래 식과 같은 제약조건을 가지게 된다.
이렇게 δ를 설정하게 되면 한가지 문제점이 생길수 있는데, 그것은 VAE의 목표인 NLL을 최소화 시키는데 제약사항이 생길 수 있다는 것이다. 하지만 다시 생각해 보면 우리의 궁극적인 목표는 NLL을 최소화하는 것이라기 보다는 Generative 모델의 성능을 높이는 것이다. NLL은 모델의 성능을 높이기 위한 하나의 수단일 뿐이다. 따라서 δ를 설정하여 모델이 더 향상될 수 있다면(Posterior Collapse를 해결할 수 있다면) NLL이 최소화 되지 못하더라고 δ를 설정하는 것이 합리적이다.
2.1 δ-VAE with Sequential Latent Variables
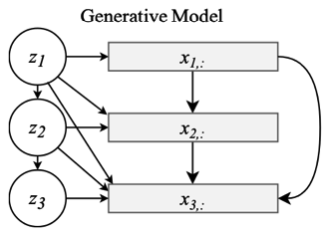
이미지, 오디오, 텍스트와 같은 데이터들은 강한 공간-시간 연속성(strong spatio-temporal continuity)를 가지고 있다. 따라서 본 논문에서는 이러한 관계를 Latent Variable들이 표현해 줏 수 있도록 Sequential Latent Varivables 방법으로 Latent variable들 간의 관계를 설정하였다. Sequential Latent Variable을 표현하기 위해서 Prior의 latent variable들은 1차 선형 autoregressive(first-order linear qutoregressive progress)한 관계를 갖는다.(Zt = αZt-1 + εs) 이 관계를 정리한 Prior는 다음과 같다.다음은 Sequential Latent Variable setting이다.
- Posterior
- Prior
위의 Posterior와 Prior 관계의 mismatch를 두 분포에 대한 KL-Dievergence의 Lower Bound로 표시하면 아래 식과 같다. 여기서 mismatch가 δ로 표현된다.
\[D_{KL}(q(z|x)||p(z)) \geq {1 \over 2} \sum_{k=1}^{d} (n-2)ln(1+\alpha_{k}^{2}) - ln(1-\alpha_{k}^{2}) = \delta\]여기서 n은 autoregressive time sequence의 길이이고, d는 latent variable의 dimension이다. 만약 d를 고정하면 δ는 n과 α로 표현할 수 있고 그 관계를 아래 그래프와 같이 표현된다.
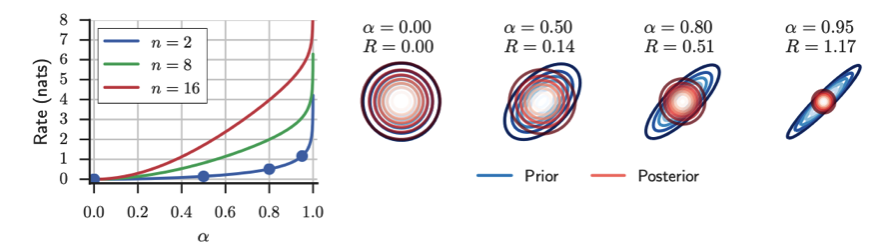
오른쪽 그림은 α가 커지면서 prior의 Autoregressive한 성질이 점정 강해지고(즉, prior latent variable들 간의 correlation이 커진다.) 있는 것을 표현한 것이다. 그리고 correlation이 증가할 수록 δ도 증가하는 것을 확인할 수 있다.
2.2 Anti-Causal Encoder Network
2.1에서 Latent Variable들을 Autoregressive한 관계로 설정해 주었는데 Encoder에서도 과거에 대한 정보를 이용하는 설정을 해준다면, 이것은 낭비가 될 것이다. 따라서 본 논문에서는 Anti-Causal Encoder 구조를 제안하였다 이것은 과거가 아닌 미래의 input data x를 이용하여 Encoder를 구성해 주는 것이다. 그 구조에 대한 그림은 다음과 같다.
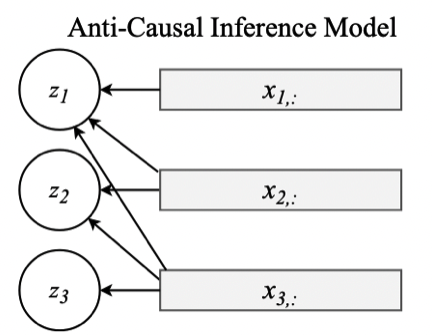
3. Experiments
4.1 Natural Images
CIFAR-10, Downsampled ImageNet을 이용하여 실험을 진행하였다. 이미지에 대한 δ-VAE에 대한 구조를 decoder와 encoder로 나눠서 살펴보면 다음과 같다.
- Decoder Decoder에서는 PixelSNAIL, GatedPixelCNN과 같은 강력한 Autoregressive 모델을 사용하였다. 본 논문에서 보여주고자 하는 것 중 하나가 강력한 Decoder를 사용하더라도 Posterior Collapse가 발생하지 않도록 하는 것 이었으므로, 합리적인 Design Choice라고 생각된다.
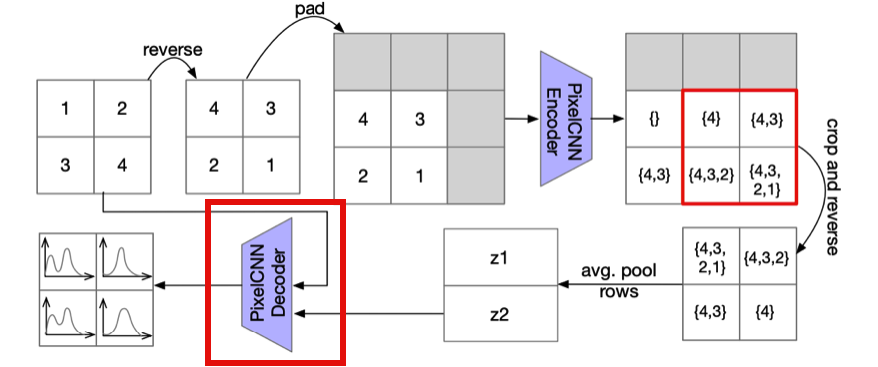
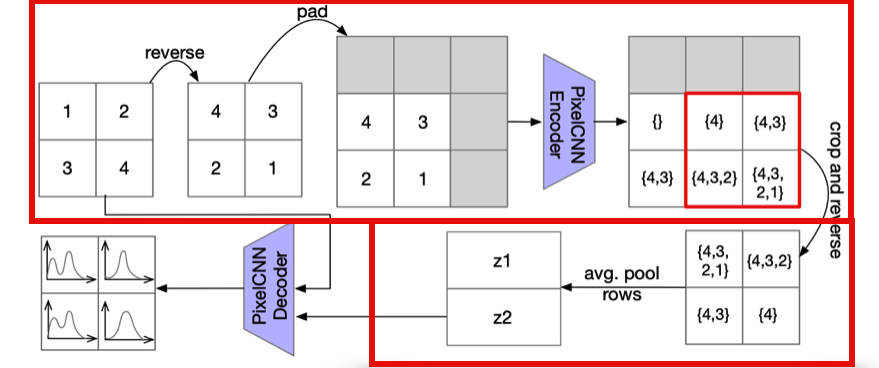
- Encoder Encoder에서는 아래 그림과 같이 일련의 과정들을 이용하여 Latent Variable로 Encoding하고 있다. 여기에서 처음에 reverse하는 부분은 2.2절에서 소개했던 Anti-Causal Encoder Network를 구현하기 위함이다.
4.2 Density Estimation Results
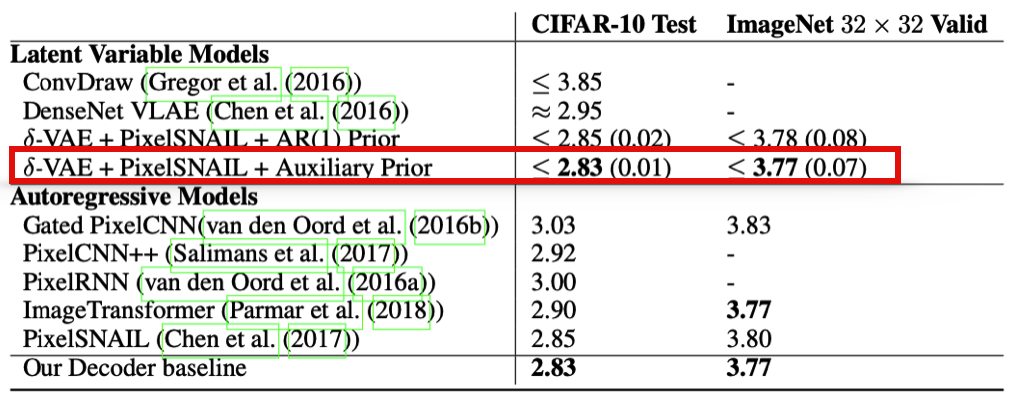
위 표는 prior work들과 negative log-likelihood를 비교한 결과이다. 여러 Latent Varible models과 Autoregressive Models을 비교하였을 때 δ-VAE가 가장 좋은 결과를 보여주고 있다.
4.3 Utilization Of Latent Variables

본 논문에서는 Latent Variable이 실제로 global structure를 표현하는지에 대한 실험을 진행하였다. 위 그림은 Latent Variable을 동일하게 하고 다양한 Decoder를 사용하여 이미지를 생성한 결과이다. 맨 왼쪽 줄을 예로 들면 전체적인 초록색 잔디의 형태는 유지한채 가운데 동물의 그림만 변하고 있는 것을 볼 수 있다. 즉, Latent Variable은 global한 구조를, autoregressive decoder는 local한 패턴을 만들어 내고 있다는 것을 알 수 있다.
4.4 Ablation Studies
- δ-VAEs
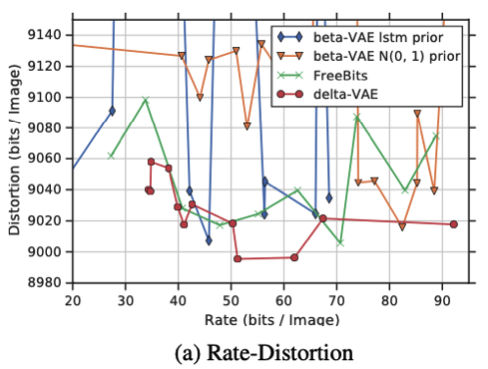
δ-VAEs를 다른 모델들(베타 VAE)과 비교하였다. 위 그래프를 보면 다른 모델들에 비해서 δ-VAEs의 Distortion이 더 낮고, 안정적인 것을 볼 수 있다.
- anti-causal encoder structure

위 표는 4개의 다른 구조 모델로 train한 결과이며, Anti-causail encoder의 성능을 보여준다. 처음 두 열은 anti-causal encoder의 유무가 성능에 크게 영향을 미치지 않지만 마지막 두 열은 anti-causal encoder를 적용했을 때 더 좋은 성능을 보이고 있는 것을 확인할 수 있다. 이것은 크기가 큰 모델에서 anti-causal 구조가 효과를 보인다는 것을 알 수 있다.
4. Conclusions
결과적으로 본 논문에서 제안한 δ-VAE는 다음 세가지의 의의를 보인다.
- δ-VAE는 1) objective를 변경하지 않고, 2) decoder를 약화시키지 않으면서 posteior collapse 문제를 해결하였다.
- posterior collapse를 해결 한 방법이 간단하다.(committed rate)
- δ-VAE는 비교 모델 중에 가장 좋은(state-of-the-art) 성능을 보였다.
5. Future Work
- 본 논문에서는 Anti-Causal Encoder + Sequential Latent Variable와 Anti-Causal Encoder + Auxiliary prior의 조합으로 실험을 진행하였다. 다만 design을 어떻게 하느냐에 따라서 posterior-prior 조합은 다양하게 나올 수 있기 때문에, 이 다양한 조합에 대한 실험을 future work로 남겨두었다.
- 본 논문에서 Posterior Collapse를 많이 개선하였지만, Posterior Collapse는 여전히 완전히 해결된 문제는 아니다. 따라서 Posterior Collapse에 대한 원인과 해결 방법들에 대한 연구에 대해서 관심을 가지고 봐야 할 것이다.
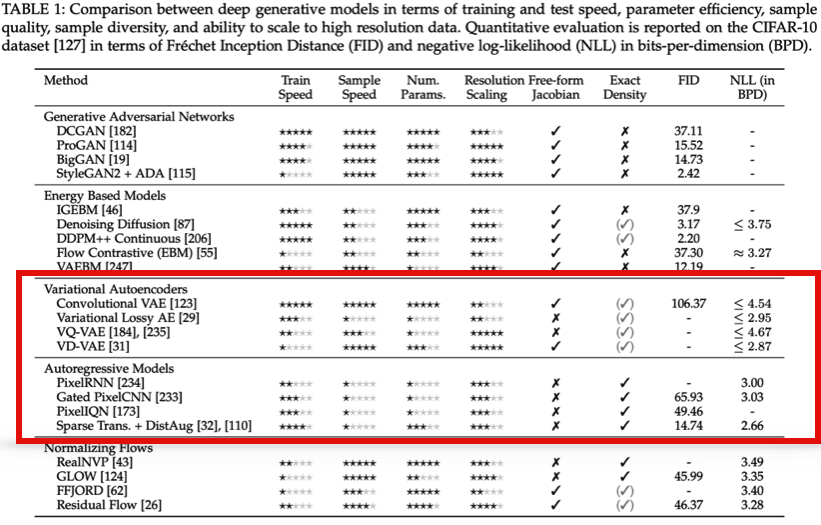
마지막으로 이 Paper에서는 Latent Variable Model이 Autoregressive Model을 성능적으로 뛰어넘을 수 있는지에 대한 challenge를 언급하였다. 이와 관련해서 아래 table은 (Sam Bond-Taylor, Adam Leach, Yang Long, Chris G. Willcocks, “Deep Generative Modelling: A Comparative
Review of VAEs, GANs, Normalizing Flows, Energy-Based and Autoregressive Models” NeurIPS 2019.)에서 가져온 Table이다. Autogregressive models, Variational Autoencoders 뿐만 아니라 다양한 Generative Model간의 비교해 두었다. 여기서 이 두 방법에 대한 장단점을 star로 표시해 두었고 마지막 부분에 NLL을 비교해 두었다. 2022년 까지 Generative Models에 대한 비교를 위해서 해당 논문을 참조하면 좋을 것 같다.
Subscribe via RSS
