original paper

Glow : Generative Flow with Invertible 1x1 convolutions

Demo

Demo


Demo Link


Abstract

Flow based generative models 장점은 다음과 같습니다.

  1. 정확한 log-likelihood를 tracking 가능합니다.
  2. 정확한 latent variable inference를 tracking 가능합니다.
  3. Training과 synthesis를 병렬화 가능합니다.

Glow의 저자는 invertible 1x1 convolution을 사용하는 generative flow model을 제안했습니다. 1x1 convolution을 사용함으로써 표준 벤치마크에서 log-likelihood가 크게 향상되었고, 큰 이미지를 효율적이고 사실적인 synthesis와 manipulation을 할 수 있습니다.

Sample img

모델 코드


1. Introduction

생성 모델링 분야에서 likelihood-based 방법들과 GAN은 엄청난 성능을 보여주었습니다. 그 중 likelihood 기반 방법은 다음과 같이 세 가지 범주로 나누면 다음과 같습니다.

  1. Autoregressive model
    • Simple 하다는 장점이 있지만 Auto Regressive하게 Generation해서 병렬화에 제한이 있습니다.
  2. Variational Auto Encoder(VAE)
    • log-likelihood의 lower bound를 최적화합니다.
    • training과 synthesis를 병렬화할 수 있지만 최적화에 어려움이 있습니다.
  3. Flow-based generative model
    • Flow-based generative model는 NICE에서 처음 설명되었고 RealNVP에서 extend 되었습니다.


Flow-based generative models은 이제까지 GAN이나 VAE에 비해 주목받지 못했으나, 논문에서는 아래와 같은 장점들을 근거로 Flow 모델을 사용했습니다.

  1. Exact latent-variable inference and log-likelihood evaluation
    • VAE: 데이터포인트에 해당하는 latent variable을 대략적으로만 추론가능합니다.
    • GAN: latent를 추론할 Encoder 없습니다.
    • Reversible generative model: latent variable inference 및 log-likelihood evalution을 approximation 없이 정확하게 수행가능합니다.
    • 따라서 데이터의 lower bound 대신 정확한 log likelihood를 최적화할 수 있습니다.
  2. Efficient inference and Efficient synthesis
    • Autoregressive model: 가역적이지만 병렬화하기 어렵고 비효율적입니다. (ex. PixelCNN)
    • Flow-based generative model: 추론과 synthesis 모두에 대해 병렬화하는 데 효율적입니다.
  3. Useful latent space for downstream tasks
    • Autoregressive model: hidden layer에 알 수 없는 marginal 분포가 있어 데이터의 유효한 조작을 하기 어렵습니다.
    • GAN: encoder가 없고 데이터 분포를 완벽하게 지원하지 않을 수 있으므로 일반적으로 latent space에서 직접 표현할 수 없습니다.
    • Reversible generative model & VAE: 유용한 latent space로 인해 datapoints 간의 interpolation과 meaningful modification이 가능합니다.
  4. Significant potential for memory savings
    • 가역적이 신경망이므로 gradient 계산 시 constant 메모리 필요합니다.

    • 자세한 내용은 RevNet 참고바랍니다.


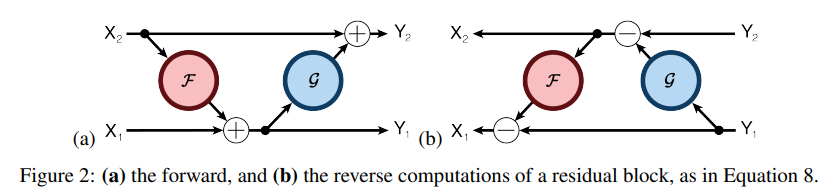
      RevNet

      출처: (https://arxiv.org/abs/1707.04585)


      • RevNet에 대해 간략하게 설명하자면, reversible block을 이용해 메모리에 activation 을 저장하지 않고 back propagation을 할 수 있는 네트워크입니다.

      • 참고: (https://arxiv.org/abs/1707.04585)


Glow 아이디어

  1. Batchnorm -> actnorm
    batch norm을 사용해 큰 이미지를 학습하는 경우, 메모리 제약으로 인해 mini batch를 1로 설정해야 하는 상황이 생겨 성능이 떨어지는 문제점이 존재합니다. 논문에서는 mini batch를 작게 설정해야하는 경우에도 훈련이 잘되도록 하는 actnorm의 사용을 제안했습니다.

  2. Reverse ordering -> 1x1 convolution
    NICE와 RealNVP에서 reverse ordering 사용해 channel의 순서에 변화를 주었지만, Glow에서는 이 부분을 1x1 convolution으로 대체해 더 낮은 NLL값을 얻었고 기존보다 더 풍부한 표현이 가능한 모델을 만들었습니다.

  3. Affine coupling layers RealNVP에서의 affine coupling layer에 (1) zero initialization와 (2) permutation을 추가해 학습 성능을 향상시켰습니다.


2. Background: Flow-based Generative Models

Change of Variable (블로그 참조)

수학에서 어떠한 변수 또는 다변수로 나타낸 식을 다른 변수 또는 다변수로 바꿔 나타내는 것을 변수 변환(Change of Variable)이라고 합니다. (위키백과 참조) 어떠한 랜덤 변수 $x$와 랜덤변수 $z$에 대해 다음과 같은 확률 밀도 함수(Probability Density Function, PDF)가 있다고 가정해봅시다. \(x⁓p(x)\) \(z⁓π(z)\)

여기서

  1. 변수 $z$가 변수 $x$를 잘 표현하는 latent variable이고 $z$의 PDF가 주어진다면, 일대일 매핑함수 $x=f(z)$를 사용해서 새로운 landom variable를 구할 수 있지 않을까?
  2. 함수 $f$가 invertible이라고 가정한다면(=역함수가 존재한다면) $z=f^{-1}(x)$도 가능하지 않을까?

라는 가정에서 출발하면 ⇒ 우리가 구할 것은 알려지지 않은 $x$의 확률 분포 $p(x)$를 구하는 것입니다.

확률분포 정의에 대해 먼저 적어보면 확률 밀도 함수의 적분은 1이 됩니다.

\[∫p(x)dx = ∫π(z)=1\]

⇒ 그러므로 두 PDF $p(x),π(z)$의 적분은 둘 다 1이 되는 것을 알 수 있습니다.

위의 정의에 변수 변환(Change of Variable)을 적용하면 다음과 같이 변하게 되고,

\[∫p(x)dx=∫π(f^{-1}(x))df^{-1}(x)\]

위 식을 미분하여 한번 더 정리하면

\[p(x)=π(z)|\frac{dz}{dx}|=π(f^{-1}(x)|\frac{df^{-1}}{dx}|)=π(f^{-1}(x))|(f^{-1})'(x)|\]

이렇게 함으로써 알지 못하는 $p(x)$를 $z$의 PDF $π(x)$로 표현할 수 있게 되었습니다. 위의 식을 조금 더 직관적으로 설명하면 서로 다른 변수 $x,z$의 밀도 함수들간의 관계는 $|(f^{-1})’(x)|$ 만큼의 비율을 갖는다고 볼 수 있습니다.

우리는 이러한 식들을 다음과 같은 방법으로 다변수 관점, 즉 행렬로 다시 표현할 예정입니다.

  1. 변수 $x,z$를 vector 표기로 바꾸어 $\mathbf{x}, \mathbf{z}$로 표시
  2. 행렬의 미분은 행렬의 형태로, 이러한 도함수 행렬을 자코비안 행렬(Jacobian Matrix)라고 함
\[\mathbf{z}⁓ π(\mathbf{z}), \mathbf{x}=f(\mathbf{z}), \mathbf{z}=f^{-1}(\mathbf{x})\] \[p(\mathbf{x})=π(\mathbf{z})|det\frac{d\mathbf{z}}{d\mathbf{x}}|=π(f^{-1}(\mathbf{x}))|det\frac{df^{-1}}{d\mathbf{x}}|\]

Jacobian Matrix and Determinant

  1. 행렬의 미분 = 도함수 행렬 = 자코비안 행렬의 정의는 벡터 $\mathbf{x}, \mathbf{y}$ 에 대한 일차 편미분(∂)을 행렬로 나타낸 것입니다. 이를 나타내면 다음과 같습니다.

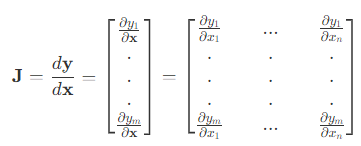
    이는 $n$차원 입력 벡터 $\mathbf{x}$를 $m$차원 출력 벡터 $\mathbf{y}$로 매핑하는 함수가 주어지면 이 함수의 모든 1차 편미분 함수 행렬을 Jacobian Matrix로 간단하게 표현할 수 있습니다.

  2. 행렬식(Determinant)은 정방행렬(n x n matrix)에 스칼라를 대응하는 함수의 하나이고 다시 말하면 행렬을 대표하는 하나의 스칼라로 계산한다는 것

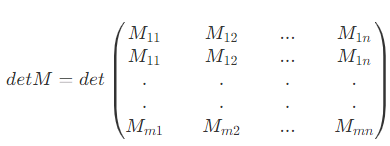
    또는

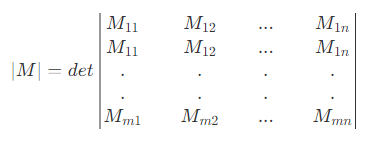
    행렬식의 주요성질은 다음과 같습니다.

    1. $det(1_{n⨉n})=1$
    2. $det(MN)=detMdetN$
    3. 행렬 $M$이 가역행렬(invertible matrix, 역행렬이 있는 행렬)인 경우, $detM≠0$
    4. 행렬 $M$이 가역행렬 인 경우, $detM^{-1}=(detM)^{-1}$
    5. $det(M^T)=detM$

    → 이를 이용하여 자코비안 행렬과 행렬식으로 전개한 수식 중 $|det\frac{df^{-1}}{d\mathbf{x}}|$ 를 해결할 수 있습니다.

역함수 정리, 가역함수의 자코비안

  1. 역함수 이론

    만약 $y=f(x)$와 $x=f^{-1}(y)$가 있다면

    \[\frac{df^{-1}}{dy}=\frac{dx}{dy}=(\frac{dy}{dx})^{-1}=(\frac{df(x)}{dx})^{-1}\]

    ⇒ 역함수의 미분과 함수의 미분은 inverse관계 ⇒ 따라서 역함수의 자코비안을 함수의 자코비안의 inverse로 표현 가능하다는 것을 알 수 있습니다.

  2. 가역함수의 자코비안

    가역행렬인 경우 행렬식 특성들을 가집니다.

    \[det(M^{-1})=(det(M))^{-1}\] \[det(M)det(M^{-1})=det(M·M^{-1})=det(I)=1\]

Normalizing flow

위에서 $\mathbf{x}$에 대한 확률밀도 함수 $p(\mathbf{x})$를 latent variable라고 가정한 $\mathbf{z}$를 이용해 추정할 수 있음을 확인하였습니다. 하지만, 좋은 $p(\mathbf{x})$를 추정한다는 것(=density estimation)은 쉽지 않습니다. 실제 딥러닝 생성 모델들은 posterior distribution $p(\mathbf{z}|\mathbf{x})$를 비교적 간단한 확률분포로 가정하거나 근사(일반적으로 가우시안 분포가 사용됨)하기 때문입니다. 그 이유는 실제 데이터 분포 $p(\mathbf{x})$는 굉장히 복잡하기 때문에 적어도 latent variable의 확률분포가 단순해야지 back propagation 계산을 조금이라도 더 쉽게 할 수 있기 때문입니다.

Normalizing Flow는 실제 데이터의 복잡한 확률 분포를 예측하는 데 있어서 효과적인 방식 중 하나입니다. 앞에서 어떤 확률 분포에 역변환 함수를 적용해서 새로운 확률 분포로 변환할 수 있는 것을 확인하였기 때문에 Normalizing Flow의 아이디어는 단순한 확률 분포에서부터 일련의 역변환 함수를 적용하여 점차 복잡한 확률 분포로 변환해나가는 것입니다. 이런 일련의 변환과 Change of Variable이론을 통해 우리는 단순한 분포로부터 새로운 변수들을 반복해서 대체하고 결과적으로 목표하는 최종 변수의 확률 분포를 얻을 수 있게 됩니다.

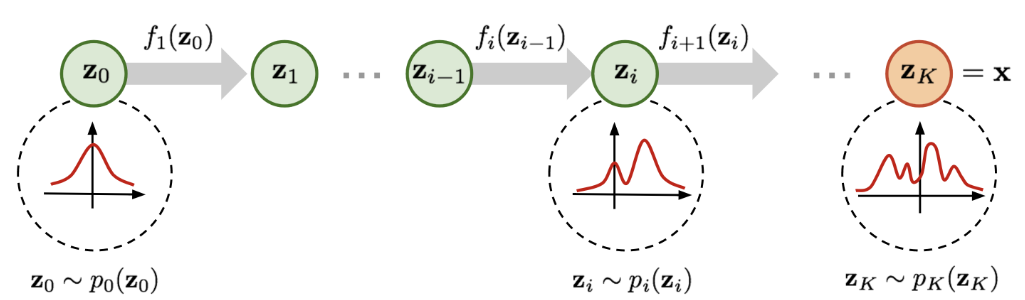
flow-based generatibe models

(출처 : Flow-based Deep Generatibe Models)

위의 그림을 수식으로 나타내면

\[\mathbf{z_{i-1}} ⁓ p_{i-1}(\mathbf{z_{i-1}}), \mathbf{z_{i}}=f_{i}(\mathbf{z_{i-1}}), 　thus 　\mathbf{z_{i-1}}=f_{i}^{-1}(\mathbf{z_{i}})\] \[p_i(\mathbf{z_{i}})=p_{i-1}(f_{i}^{-1}(\mathbf{z}_{i}))|det\frac{df_i^{-1}}{d\mathbf{z}_i}|\]

이 수식은 위에서 정리했던 수식 $p(\mathbf{x})=π(\mathbf{z})|det\frac{d\mathbf{z}}{d\mathbf{x}}|=π(f^{-1}(\mathbf{x}))|det\frac{df^{-1}}{d\mathbf{x}}|$ 과 동일한 것을 볼 수 있습니다. 달라진 점은 연속된 역변환을 나타내기 위해 $i$번째 변수와 확률 분포 그리고 역변환을 표시한 것 뿐 입니다.

이 수식을 조금 더 정리하면

수식정리

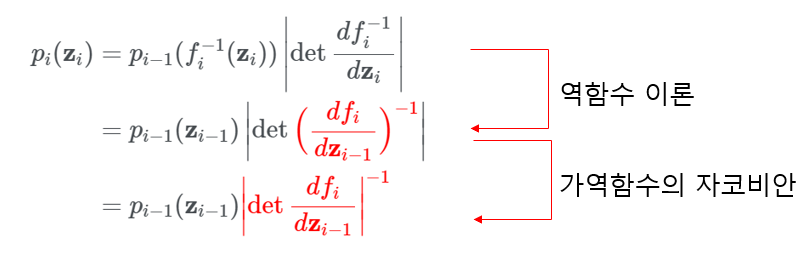
이를 다시 보기 좋게 정리하면

\[logp_{i}(\mathbf{z_{i}})=logp_{i-1}(\mathbf{z_{i-1}})-log|det\frac{df_{i}}{d\mathbf{z_{i-1}}}|\]

마지막에 $log$를 취한 이유는 확률 등의 수식에서 곱셈이 나올 때 전체적으로 $log$를 취해주면 대부분은 곱을 합으로 바꿀 수 있어서 계산이 쉬워지기 때문입니다.

위의 내용들을 이용하여 $\mathbf{z}_0$의 확률 분포에서부터 시작해 $K$번의 역변환을 통해 $\mathbf{x}$의 확률분포를 구하는 수식을 정리할 수 있습니다.

\[\mathbf{x}=\mathbf{z_{K}}=f_{K}ºf_{K-1}º···ºf_{1}(\mathbf{z_{0}})\]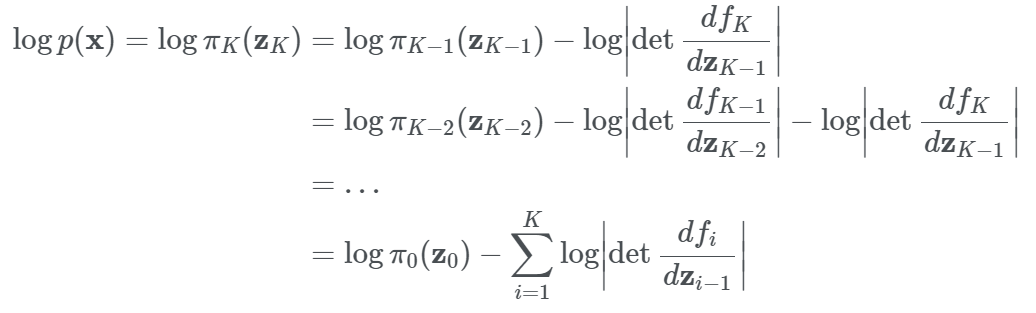

Untitled

위와 같이 $logp(\mathbf{x})$를 정의한 후 우리가 가지고 있는 학습 데이터셋 $D$ 에 대해 NLL(Negative Log-Likelihood)를 만들면

\[\mathcal{L}(\mathcal{D})=-\frac{1}{|\mathcal{D}|}\sum_{x∈\mathcal{D}}{logp(\mathbf{x})}\]

3. proposed Generative Flow

actnorm 단계 → invertible 1x1 convolution 단계 → affine couplint layer 단계 총 3단계를 거치며 이 flow는 Multi-scale architecture에 결합이 되는 것을 아래 그림에서 확인할 수 있습니다.

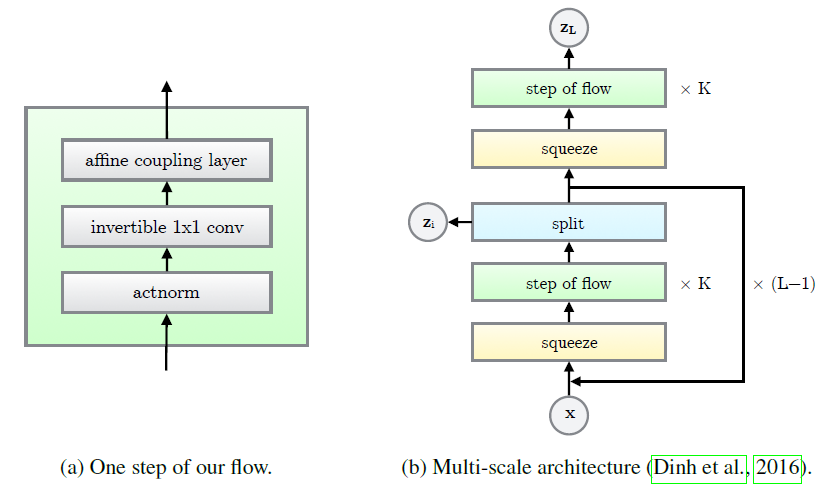
Untitled

3.1. Actnorm : scale and bias layer with data dependent initialization

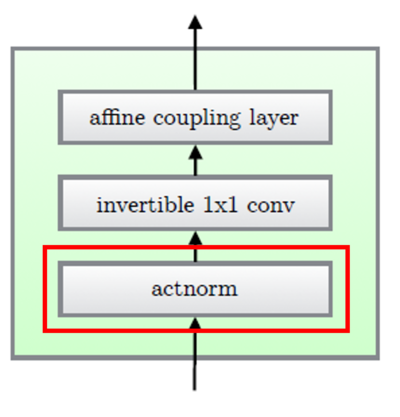
Untitled

이 step에서는 scale과 bias parameter로 affine transform을 진행합니다.

Actnorm은 기존의 RealNVP에서 사용하였던 batchnorm을 대체하여 사용하는 것입니다. batchnorm은 한 GPU 혹은 PU당 처리하는 minibatch size가 클 수록 효과가 좋은데 큰 이미지에서는 메모리 제약으로 인해 minibatch size를 크게 할 수 없어 minibatch size를 1로 훈련해야 합니다. 한 마디로 minibatch 클 수록 효과 좋은데 큰 이미지에서는 제일 작은 1로밖에 훈련 못해서 성능이 좋지가 않습니다. 하지만 actnorm이 이를 극복하여 minibatch size가 1일때도 훈련이 잘 되도록 하였습니다. 그 이유는 첫 번째 minibatch의 mean과 variance로 초기화한 parameter로 normalization을 진행하고 초기화된 이후에는 데이터와 독립된 trainable parameter로 취급되기 때문입니다.

batchnorm과 actnorm의 차이에 대해 조금 더 명확하게 설명하자면 batchnorm이 data에서 연산한 running statistics를 통해 normalization을 수행한다면, actnrom은 첫 번째 batch에서 연산한 statistics로 초기화한 파라미터를, 이후에는 독립적인 trainable parameter로 상정하고 normalization을 진행한다는 점에서 차이가 존재합니다.

actnorm은 channel-wise normalization을 수행합니다. 즉, $h×w×c$ 의 image tensor가 주어지면 channel dimension에서 동작합니다.

실제 Glow에서 사용한 코드를 확인하면 다음과 같습니다.

def actnorm(name, x, scale=1., logdet=None, logscale_factor=3., batch_variance=False, reverse=False, init=False, trainable=True):
    if arg_scope([get_variable_ddi], trainable=trainable):
        if not reverse:
            x = actnorm_center(name+"_center", x, reverse)
            x = actnorm_scale(name+"_scale", x, scale, logdet,
                              logscale_factor, batch_variance, reverse, init)
            if logdet != None:
                x, logdet = x
        else:
            x = actnorm_scale(name + "_scale", x, scale, logdet,
                              logscale_factor, batch_variance, reverse, init)
            if logdet != None:
                x, logdet = x
            x = actnorm_center(name+"_center", x, reverse)
        if logdet != None:
            return x, logdet
        return x

변수 x를 centering과 scaling을 하는 convenience function을 사용하여 actnorm이 필요할 때 이 함수를 호출하여 사용합니다.

3.2. Invertible 1 × 1 convolution

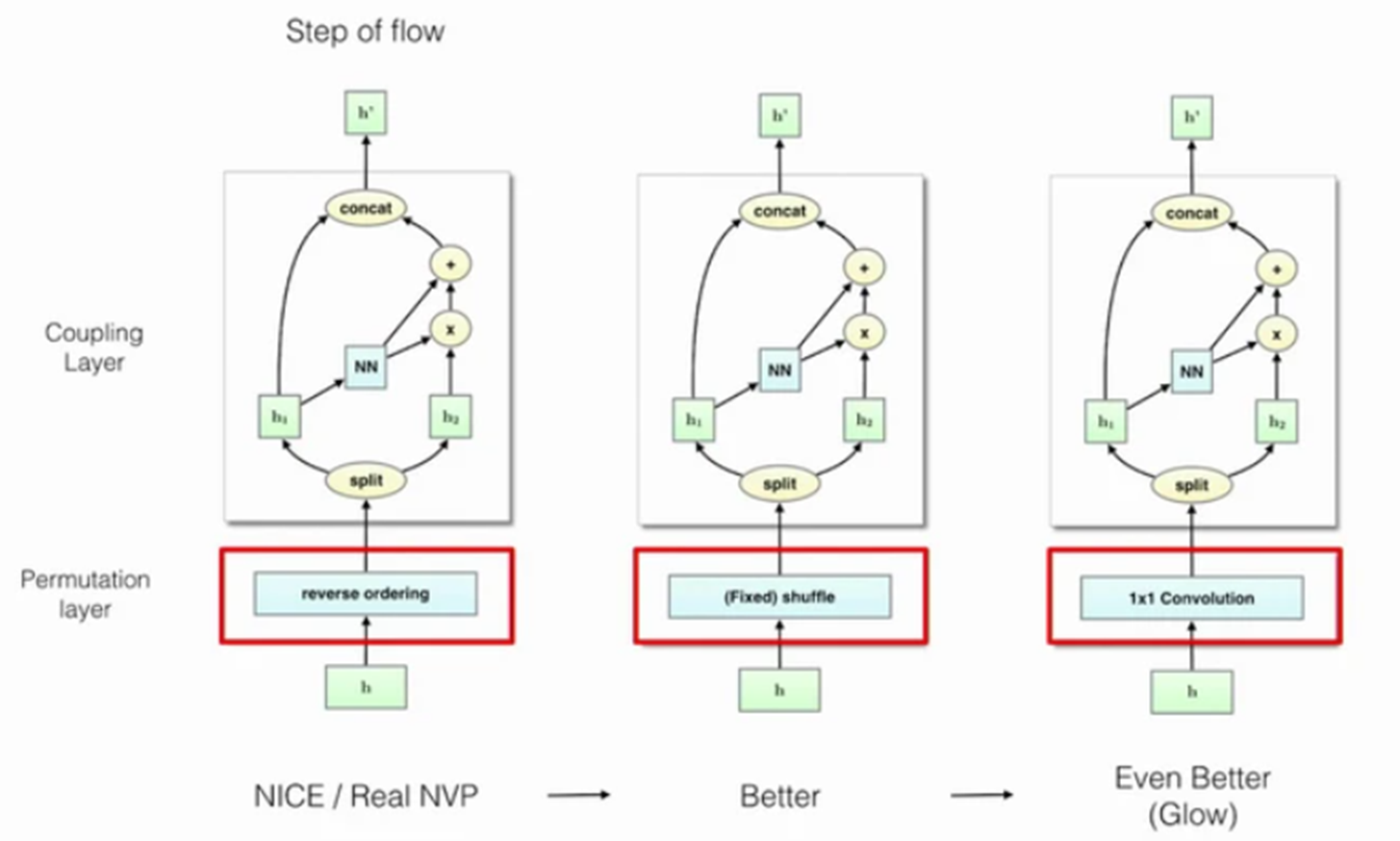
Untitled

출처: (https://crossminds.ai/video/glow-generative-flow-with-invertible-1x1-convolutions-60774dd2825a3436b95eeded/)

위의 그림을 보면 알 수 있듯이 NICE와 RealNVP는 단순히 reverse ordering하는 형태로 순서를 바꿔주었습니다. 근데, Glow의 저자들이 reveser ordering 대신 suffle을 했더니 더 좋은 성능(NLL)이 나왔고, 대신에 1x1 convolution을 진행했더니 그보다 더 나은 성능임을 확인하여 이 논문에서는 1x1 convolution에 대해 설명하고 있습니다.

조금 더 직관적으로 비교하자면 이전에는

\[\begin{bmatrix} 0 \\ 1 \end{bmatrix}\]

혹은

\[\begin{bmatrix} 1 \\ 0 \end{bmatrix}\]

과 같은 단순히 순서를 바꾸는 matrix를 이용하였다면 이 논문에서는

\[\begin{bmatrix} cosθ&&sinθ \\ -sinθ&&cosθ \end{bmatrix}\]

와 같은 rotation matrix를 사용, 더 풍부한 표현을 가능하게 했다고 말하고 있습니다. 더 범용적으로 사용가능하기 때문에 “순열의 일반화(=generalization of a permutation operation)”라는 표현을 논문에서 여러번 언급하고 있습니다.

log-determinant of layer

이러한 random rotation matrix를 weighted matrix $W$로 사용, invertible 1x1 convolution의 log-determinant는 determinant of weight matrix $W$로 귀결되며 다음과 같이 정리됩니다.

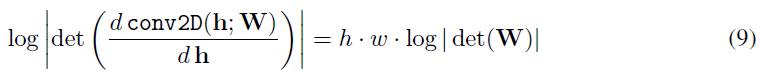
Untitled

처음에는 가중지 $W$를 log-determinant가 0인 randome rotation matrix로 초기화 한 후, 한 SGD단계 후에 이 값은 0에서 발산하기 시작합니다. 여기서의 문제는 weight Matrix $W$의 determinant 연산이 $O(c^3)$의 비용이 들어 channel이 커질수록 intractable한 문제가 발생하는데, 그래서 저자는 LU Decompostion을 사용을 하게 됩니다.

LU Decompostion

$det(W)$의 계산 비용을 LU Decompostion을 통해 $O(c^3)$ 에서 $O(c)$로 줄이기 위해 이러한 방법을 채택하였습니다.

Untitled

여기서 $P$는 단순히 LU 분해를 용이하게 하기 위한 permutation matrix라고 생각하면 되는데, 이때 기존 LU Decompostion 공식에 따르면 $W=PLU$로 분해되어야 맞습니다. 하지만 여기서 저자는 상부삼각행렬인 $U$를 대각성분과 그 나머지로 한 번 더 분리합니다. 그렇게 하였더니 log-determinant를 다음과 같이 간단하게 계산할 수 있게 되었습니다. 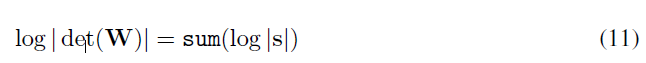Untitled LU decompostion을 했을 때와 하지 않았을 때 wall-clock 계산 시간의 큰 차이를 측정하지는 않았지만, 계산 비용의 차이는 큰 $c$에 대해서는 확실히 중요해질 것이라고 말하고 있습니다.

1x1 convolution에 관련된 코드는 다음과 같습니다.

def invertible_1x1_conv(name, z, logdet, reverse=False):
    if True:  # Set to "False" to use the LU-decomposed version
        with tf.variable_scope(name):

            shape = Z.int_shape(z)
            w_shape = [shape[3], shape[3]]

            # Sample a random orthogonal matrix:
            w_init = np.linalg.qr(np.random.randn(
                *w_shape))[0].astype('float32')

            w = tf.get_variable("W", dtype=tf.float32, initializer=w_init)

            # dlogdet = tf.linalg.LinearOperator(w).log_abs_determinant() * shape[1]*shape[2]
            dlogdet = tf.cast(tf.log(abs(tf.matrix_determinant(
                tf.cast(w, 'float64')))), 'float32') * shape[1]*shape[2]

            if not reverse:
                _w = tf.reshape(w, [1, 1] + w_shape)
                z = tf.nn.conv2d(z, _w, [1, 1, 1, 1],
                                 'SAME', data_format='NHWC')
                logdet += dlogdet

                return z, logdet
            else:
                _w = tf.matrix_inverse(w)
                _w = tf.reshape(_w, [1, 1]+w_shape)
                z = tf.nn.conv2d(z, _w, [1, 1, 1, 1],
                                 'SAME', data_format='NHWC')
                logdet -= dlogdet

                return z, logdet

저자들은 기본적으로는 1x1 convolution 연산 시, LU Decompostion을 사용하지는 않는 것을 확인할 수 있습니다. 이론적으로 computational cost가 줄어들 수는 있지만, LU Decompostion 과정 자체가 또 다시 cost가 들기 때문입니다. 그래서 필요 시에 사용자가 다음과 같이 else문을 통하여 LU Decompostion을 사용하는 1x1 convolution 연산을 할 수 있습니다.

 else:
        # LU-decomposed version
        shape = Z.int_shape(z)
        with tf.variable_scope(name):

            dtype = 'float64'

            # Random orthogonal matrix:
            import scipy
            np_w = scipy.linalg.qr(np.random.randn(shape[3], shape[3]))[
                0].astype('float32')

            np_p, np_l, np_u = scipy.linalg.lu(np_w)
            np_s = np.diag(np_u)
            np_sign_s = np.sign(np_s)
            np_log_s = np.log(abs(np_s))
            np_u = np.triu(np_u, k=1)

            p = tf.get_variable("P", initializer=np_p, trainable=False)
            l = tf.get_variable("L", initializer=np_l)
            sign_s = tf.get_variable(
                "sign_S", initializer=np_sign_s, trainable=False)
            log_s = tf.get_variable("log_S", initializer=np_log_s)
            # S = tf.get_variable("S", initializer=np_s)
            u = tf.get_variable("U", initializer=np_u)

            p = tf.cast(p, dtype)
            l = tf.cast(l, dtype)
            sign_s = tf.cast(sign_s, dtype)
            log_s = tf.cast(log_s, dtype)
            u = tf.cast(u, dtype)

            w_shape = [shape[3], shape[3]]

            l_mask = np.tril(np.ones(w_shape, dtype=dtype), -1)
            l = l * l_mask + tf.eye(*w_shape, dtype=dtype)
            u = u * np.transpose(l_mask) + tf.diag(sign_s * tf.exp(log_s))
            w = tf.matmul(p, tf.matmul(l, u))

            if True:
                u_inv = tf.matrix_inverse(u)
                l_inv = tf.matrix_inverse(l)
                p_inv = tf.matrix_inverse(p)
                w_inv = tf.matmul(u_inv, tf.matmul(l_inv, p_inv))
            else:
                w_inv = tf.matrix_inverse(w)

            w = tf.cast(w, tf.float32)
            w_inv = tf.cast(w_inv, tf.float32)
            log_s = tf.cast(log_s, tf.float32)

            if not reverse:
                w = tf.reshape(w, [1, 1] + w_shape)
                z = tf.nn.conv2d(z, w, [1, 1, 1, 1],
                                 'SAME', data_format='NHWC')
                logdet += tf.reduce_sum(log_s) * (shape[1]*shape[2])
                return z, logdet

            else:
                w_inv = tf.reshape(w_inv, [1, 1]+w_shape)
                z = tf.nn.conv2d(
                    z, w_inv, [1, 1, 1, 1], 'SAME', data_format='NHWC')
                logdet -= tf.reduce_sum(log_s) * (shape[1]*shape[2])
                return z, logdet

3.3. Affine Coupling Layers

layer 자체는 RealNVP에서 제안된 layer와 동일합니다.
간단하게 설명하고 넘어가자면 1~d까지의 차원은 그대로 가져가고 d+1~D까지의 차원은 scale and shift를 하는 affine transform을 취하는 형태입니다. 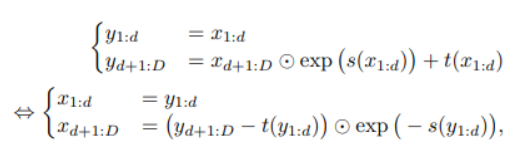Untitled 아래 그림을 통해 쉽게 back propagation이 가능함을 알 수 있음

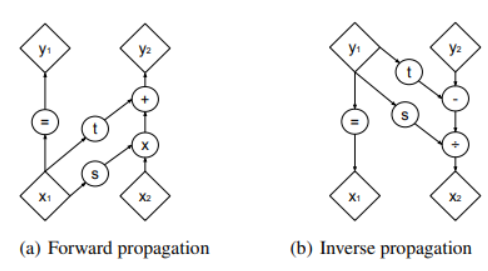
Untitled

layer 자체는 동일하지만 Glow에서는 두 가지 trick을 추가하였습니다.

  1. Zero initialization

    couplint layer는 affine transform에 활용할 parameter를 NN()을 통해 연산을 합니다. 이 때 NN()이후 추가 convolution을 하나 더 두고 이것의 weight를 0으로 두어 학습 초기에 identify function이 되도록 만듭니다. 이렇게 하면 매우 깊은 네트워크의 학습에 도움을 준다고 저자는 말하고 있습니다.

    zero initialization 코드는 다음과 같습니다.

     def linear_zeros(name, x, width, logscale_factor=3):
     with tf.variable_scope(name):
         n_in = int(x.get_shape()[1])
         w = tf.get_variable("W", [n_in, width], tf.float32,
                             initializer=tf.zeros_initializer())
         x = tf.matmul(x, w)
         x += tf.get_variable("b", [1, width],
                             initializer=tf.zeros_initializer())
         x *= tf.exp(tf.get_variable("logs",
                                     [1, width], initializer=tf.zeros_initializer()) * logscale_factor)
         return x

    이를 사용하는 곳은 다음과 같습니다.

     def prior(name, y_onehot, hps):

     with tf.variable_scope(name):
         n_z = hps.top_shape[-1]

         h = tf.zeros([tf.shape(y_onehot)[0]]+hps.top_shape[:2]+[2*n_z])
         if hps.learntop:
             h = Z.conv2d_zeros('p', h, 2*n_z)
         if hps.ycond:
             h += tf.reshape(Z.linear_zeros("y_emb", y_onehot,
                                         2*n_z), [-1, 1, 1, 2 * n_z])

         pz = Z.gaussian_diag(h[:, :, :, :n_z], h[:, :, :, n_z:])

     def logp(z1):
         objective = pz.logp(z1)
         return objective

     def sample(eps=None, eps_std=None):
         if eps is not None:
             # Already sampled eps. Don't use eps_std
             z = pz.sample2(eps)
         elif eps_std is not None:
             # Sample with given eps_std
             z = pz.sample2(pz.eps * tf.reshape(eps_std, [-1, 1, 1, 1]))
         else:
             # Sample normally
             z = pz.sample

         return z

     def eps(z1):
         return pz.get_eps(z1)

     return logp, sample, eps

    간단하게 설명하자면 0으로 채워진 tensor 생성 후 y_onehot에서 conv2d 연산 수행을 합니다. 이 후 다른 연산을 거쳐 0으로 채워진 tensor에 이를 추가합니다. 단순히 weight를 0으로 만들어 넘겼다고 논문에서 설명하고 있지만, 실제로는 zero_initialization의 원리를 이용하여 딥러닝에서 발생할 수 있는 문제를 해결했다고 보시면 될 것 같습니다.

  2. permutation

    NICE에서는 split 함수로 입력 tensor를 채널차원을 따라 두 개의 절반으로 분할하고, concat 연산은 해당 연산의 역 연산을 수행하여 단일 tensor로 연결하는 방식을 채용하였고, RealNVP에서는 NICE와는 다른 유형의 분할이 도입 되었는데, checkboard pattern을 사용하여 공간 차원을 따라 분할을 합니다.

    Glow는 invertible 1x1 convolution을 통해 permutation의 일반화된 표현을 사용하기 때문에 RealNVP와 같은 checkboard pattern 형식의 mask가 큰 의미가 없어서 단순히 channel을 split하고 concat하는 방식을 가져왔습니다.(이 부분은 NICE것을 차용했다고 생각하면 됨!)


4. Related Work

Glow (Generative Flow with Invertible 1x1 Convolutions)

  • Glow는 NICE와 RealNVP를 기반으로 더 발전된 모델입니다.
  • Sampling하는데 적은 시간이 걸립니다. (ex. 256x256 image takes less than 1 second)

MAF (Masked Autoregressive Flow for Density Estimation)

  • IAF (Inverse Autoregressive Flow) 기반 모델입니다.
  • 병렬화 불가로 인해 비효율적입니다.

Auto Regressive models

  • (ex) PixelRNN, WaveNet etc..
  • 병렬화 불가 및 고차원 데이터 합성 시 시간이 오래걸립니다.

GAN (Generative Adversarial Networks)

  • 일반적으로 latent-space encoder에 결핍이 있습니다.
  • 일반적으로 full support over the data에 결핍이 있습니다.
  • optimization에 어려움이 있습니다.
  • overfitting 및 generalization 평가 어렵습니다.


5. Experiment

Performance


Table 2


CIFAR-10, ImageNet 등의 데이터 셋에서 Glow가 Real NVP보다 좋은 성능을 보입니다. Table의 가장 마지막 행에는 Real NVP논문에서 나온 PixelRNN의 값입니다. Glow의 성능이 PixelRNN에 비해서는 떨어졌지만, Resolution이 커지면서 그 격차가 작아지는 경향을 보입니다. 위 Table에 나와있진 않지만 PixelRNN은 sequential하기 때문에 오랜 시간이 걸리고 Glow는 이와 비교해 적은 시간이 걸린다는 점을 고려하면 괜찮은 성능을 보인다고 생각합니다.

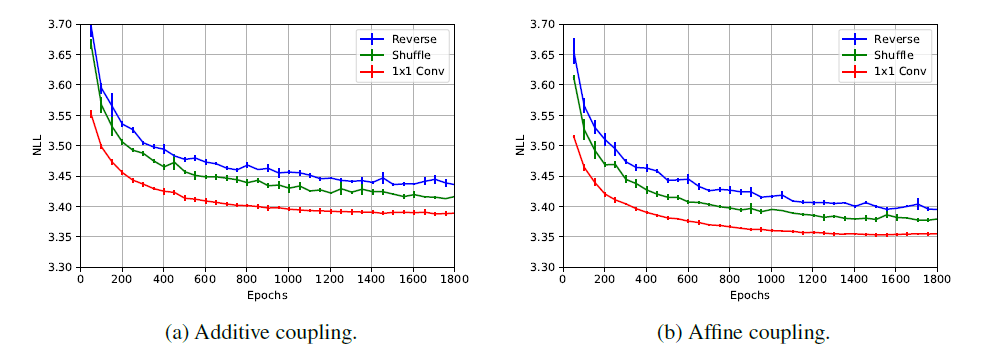
performance

1x1 convolution을 reverse, shuffle과 비교한 그래프입니다. 1x1 convolution을 사용한 경우, 더 안정적이게 높은 성능을 보이는 것을 확인할 수 있습니다.


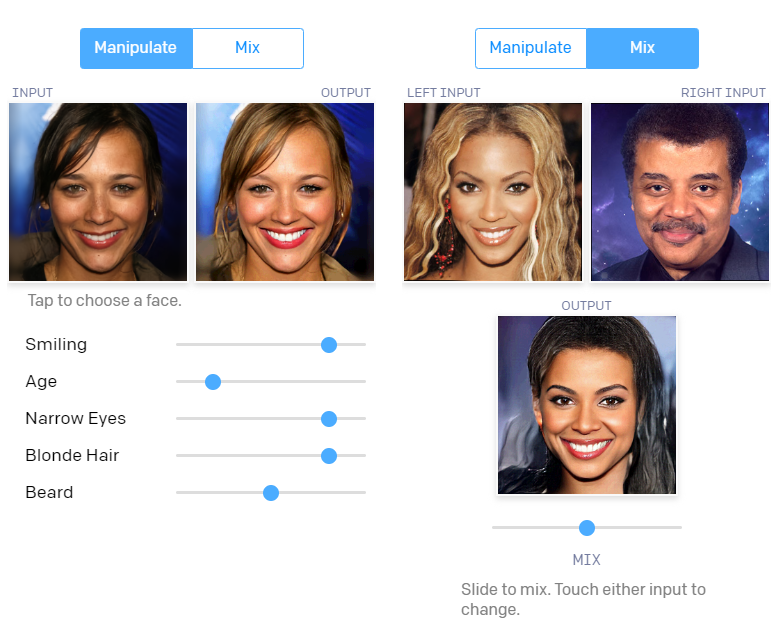
Interpolation & Manipulation

Interpolation

Interpolation

Real image pair 에서 latents를 계산해, Interpolation하면 위의 이미지와 같은 결과를 얻을 수 있습니다. 논문에서는 위 결과를 통해, manifold 가 smooth하고 중간단계들의 얼굴이 실제 얼굴처럼 보인다고 주장합니다.


Manipulation

Manipulation

Manipulation에서도 괜찮은 성능을 보이는 것을 확인할 수 있었습니다. 오른쪽 수식과 같이 attribute를 가진 latent vector에서 가지지 않은 latent vector를 빼서 manipulation 방향을 정해 결과를 구했습니다. Manipulation 영상을 보면, 특정 속성을 변경했을 때 이미지 전체가 밝아지는 경향을 보이는 등, 완전히 independent 하지는 않지만 괜찮은 성능을 보입니다.


Temperature & Model depth

Temperature

Temperature

Temperature가 클수록 (즉, 1에 가까울수록) 더 다양한 표현이 가능하지만, 너무 과하게 큰 경우 이상한 이미지가 나오는 경우가 존재합니다. 논문에서는 temperature를 0.7로 사용한 model(reduced-temperature model)이 가장 적절하다고 합니다.


Model depth

Model depth

Model depth 실험에서는 L값이 너무 작은 경우에는 feature들이 잘 안 나오는 것을 확인할 수 있습니다.


6. Future work

Flow ++

Flow++는 이전과 비교해 3가지 변경사항이 있습니다.

  1. uniform dequantization -> variational flow-based dequantization
    • Dequantization을 위해 사용하는 uniform noise는 최적의 training loss와 generalization 효과를 내지 못하므로 Variational flow-based dequantization을 사용했습니다.
  2. affine coupling flow -> logistic mixture CDF coupling flow
    • 충분히 표현력이 강하지 못한 Affine coupling flow를 logistic mixture CDF coupling flow로 변경했습니다.
  3. convolutional conditioning networks in coupling layer -> -> self-attention in the conditioning networks of coupling layers
    • 기존 Convolutional network 보다 더 강력한 self-attention in the conditioning networks로 변경했습니다.

    Flow ++

    출처: (https://arxiv.org/abs/1902.00275)

성능적인 측면에서 Flow++은 CIFAR 10, ImageNet 데이터 셋에서 Glow보다 더 높은 성능을 보입니다.


FFJORD (Free-form Jacobian of Reversible Dynamics)

Limited model -> Free form model

이전 모델들은 points 매핑할 때 invertible neural network를 이용해 simple distribution을 complex distribution으로 만들었는데 (즉, function x=f(z)의 함수 f를 복잡하게 만들었습니다.) 이때 Jacobian matrix 계산을 쉽게 하기 위해 모델의 architecture를 제한했습니다. FFJORD에서는 Jacobian으로 부터 free form인 모델을 만들 수 있게 되었습니다.

Flow ++

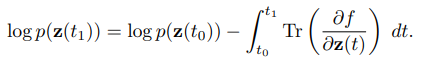
출처: (https://arxiv.org/abs/1810.01367)

Jacobian determinants 대신, Jacobian의 trace(대각합)들의 적분 값으로 이를 대체하는 방법을 사용합니다. 따라서 determinants 구할 때보다 더 낮은 time complexity를 갖게 됩니다.

Flow ++

출처: (https://arxiv.org/abs/1810.01367)

MNIST에서는 Glow보다 더 놓은 성능을 보였고, CIFAR10에서는 Glow보다는 좋지 않지만, 유사한 성능을 보였습니다.


7. Conclusion

Glow는 Auto Regressive model, VAE, GAN 등에 비해서 다소 주목받지 못했던 Flow-based generative model을 사용했습니다. Flow model의 장점인 (1) tractability of the exact log-likelihood, (2) tractability of the exact latent-variable inference, (3) parallelizability of both training and synthesis 에서 영감을 얻어 모델을 설계했습니다. Glow의 아이디어인 (1) Actnorm, (2) 1x1 convolution, (3) 변화된 Affine coupling layers을 사용해 이전 모델인 NICE와 RealNVP 보다 더욱 향상된 성능의 모델을 선보였습니다. 논문에서는 high-resolution natural 이미지를 효율적으로 합성할 수 있는 최초의 likelihood-based 모델이라고 주장합니다.

Strong points:

  1. 병렬화를 통해 high-resolution 이미지를 효율적이고 빠르게 합성할 수 있습니다.
  2. 1x1 convolution을 이용해 이전 모델보다 더 풍부한 표현이 가능합니다.

Weak Points:

  1. Jacobian matrix 계산을 쉽게 하기 위해 architecture를 제한했습니다.
  2. Jacobian determinant를 사용하기 때문에 Jacobian trace를 계산하는 것보다 더 높은 time complexity를 갖습니다.
  3. Affine coupling flow 대신 더 강력한 coupling flow를 사용하면 더 풍부한 표현이 가능할 것입니다.
  4. 1x1 convolution을 사용해 이전보다 더 풍부한 표현이 가능해졌지만, 이보다 더 강력한 network를 사용한다면 더욱 향상된 성능의 모델을 만들 수 있을 것입니다.