GAN : Generative Adversarial Nets 리뷰

안녕하세요. 최초의 GAN 논문인 Generative Adversarial Nets를 리뷰하도록 하겠습니다.

1. Background
2. Abstract
3. Introduction
4. Adversarial nets
5. Theoretical Results
6. Experiments
7. Advantages and disadvantages
8. Conclusion and future work

순으로 리뷰를 진행하도록 하겠습니다.

1. Background

1-1. 이미지와 차원(dimension) 분포(distribution) 간의 관계(블로그 참조)

먼저 한 가지 질문을 던지면서 글을 시작하겠습니다.

“이미지를 표현하기위해 필요한 차원의 수는 어떻게 될까요?”

답은 이미지의 크기에 따라 달라진다 입니다. 만약 gray scale의 튜링이미지의 크기가 200x200이라면 약 40000차원이 필요하며, 경우의 수는 10^{96329}개로 나타낼 수 있습니다.

“그렇다면, 200×200 gray scale 에서 표현될 수 있는 모든 경우의 수에 해당하는 이미지들은 의미가 있다고 할 수 있을까요?”

예를 들어, 10^{96329} 경우의 조합들 중에서 아래 왼쪽과 같이 의미 없는 이미지(noise image)들도 있을 것이고, 오른쪽 같이 사람이 구별할 수 있는 의미 있는 이미지가 있을 수 있습니다.

여기서 또 한 가지 질문을 던져볼 수 있습니다.

“200×200 gray scale 즉, 40000차원 상에서 의미있는 이미지들은 고르게 분포(uniform distribution)하고 있을까요? 아니면 40000차원이라는 공간의 특정 영역에 몰려있거나 특정 패턴으로 분포(non-uniform distribution)하고 있을까요?”

이러한 질문에 답을 하는 방법 중 하나는 200×200 gray scale 이미지들을 uniform distribution으로 수 없이 샘플링 해봐서 경험적으로 보여주는 것입니다. 만약, uniform distribution을 전제로 수 없이 샘플링 했을 때, 의미있는 이미지들이 종종 보인다면 의미있는 이미지들이 40000차원 상에 고르게 분포한다고 볼 수 있습니다.

20만번 샘플링한 결과 의미없는 이미지(noisy image)만 추출된 것을 확인 할 수 있었다고 합니다. 이러한 실험을 통해 의미있는 이미지들은 40000차원에서 특정 패턴 또는 특정 위치에 분포해 있다고 경험적으로 결론내릴 수 있게 됩니다.

1-2. Parzen Window(블로그 참조)

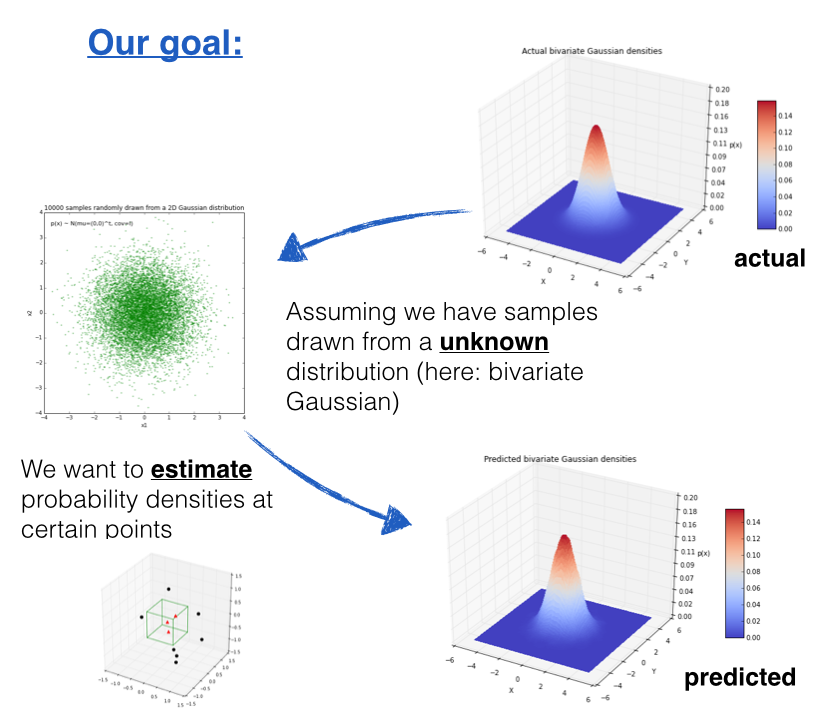
GAN의 성능 측정 방법으로 활용된 Parzen window의 확률 밀도 추정 방법에 대해 설명 드리겠습니다. Parzen Window이란 kernel method 중 고차원 데이터를 다루기 위한 대표적인 방법으로 관측된 데이터들의 분포로부터 원래 변수의 확률 분포 특성을 추정하기 위한 밀도 추정 방법입니다. GAN의 경우 implicit density model로써 사전에 분포를 특정하지 않는 방법을 사용하며, non-parametric model로써 분포를 특정 할 수 없고, 관측된 데이터만으로 확률 밀도를 구해야 하기에 Parzen Window 방법을 활용하였다고 보시면 될 것 같습니다.

2. Abstract

GAN이라는 것은 기본적으로 generative model의 성능을 높이는 것이 목적으로 generative model과 discriminator model을 경쟁 시키는 방법을 사용합니다. 이를 설명하기 위해 논문에서는 위조 지폐범과 경찰의 예시를 들었는데요. 위조지폐범은 최대한 진짜 같은 화폐를 만들어(생성) 경찰을 속이기 위해 노력하고, 경찰은 진짜 화폐와 가짜 화폐를 완벽히 판별(분류)하여 위조지폐범을 검거하는 것을 목표로 합니다. 이러한 경쟁적인 학습이 지속되다 보면 어느 순간 위조지폐범은 진짜와 다를 바 없는 위조지폐를 만들 수 있게 되고 경찰이 위조지폐를 구별할 수 있는 확률도 ½로 수렴하게 되어 경찰은 위조지폐와 실제 화폐를 구분할 수 없는 상태에 이르게 됩니다.

3. Introduction

논문에서는 CNN(=discriminative model)과 같은 딥러닝 모델이 성공한 이유를 세 가지 측면에서 설명하고 있습니다.

1. Map a high-dimensional, rich sensory input to a class label : discrimination을 위해 저차원 vector(Fc Layer의 neuro들)를 선별해줌(Curse of dimensionality 극복)
2. Backpropagation and dropout algorithms : Neural network의 첫번째 겨울을 극복하게 해준 알고리즘
3. Piecewise linear units : Neural network의 첫번째 겨울을 극복하게 해준 ReLU(Vanishing gradient 극복) ReLU는 0을 기점으로 구분적으로 linear한 성격을 가지고 있으며, Sigmoid보다 piecewise linear units(ReLU)에 의해 gradient가 더 잘 동작되었습니다.
   

Deep generative model은 CNN 만큼 큰 임팩트를 주지는 못했는데, 그 이유는

1. 계산의 복잡성 : 확률 모델을 생성하기 위해 maximum likelihood 계산을 할 때는 계산 시스템 관점에서 intractable problem 문제에 부딪히는 경우가 많음
2. ReLU와 같이 piecewise linear units의 장점을 살리기 어려움

이러한 문제를 해결하기 위해 Ian Goodfellow는 Adversarial nets를 활용한 새로운 방식을 제안하였습니다.

4. Adversarial nets(블로그 참조)

4-1. Adversarial net Architecture

아래 그림은 논문에서는 GAN Architecture가 없어서 이해를 위해 첨부하였으며, 모델 G의 학습 과정은 generator의 분포 Pg를 x에 대해 학습시키기 위해 input noise 변수에 대한 사전분포인 Pz(z)를 정의한 뒤, 노이즈변수의 데이터 공간에의 매핑을 G(Z; θg)로 만듭니다. 이때 G는 파라미터 θg를 가지는 미분가능한 다층 퍼셉트론입니다. 또한, 입력된 샘플이 Pg가 아닌 실제 데이터 분포에서 얻어졌을 확률(스칼라 값)을 계산하는 다층 퍼셉트론인 D(X; θd)를 정의합니다.

논문에서는 uniform distribution으로 input noise를 sampling 했다고 하는데, 여기서 한 가지 질문을 해보도록 하겠습니다.

“앞서, uniform sampling을 했다고 했는데, gaussian sampling을 하는건 안되나요?”

이에 대한 답을 하기 위해서는 GAN이 implicit density 방식으로 사전에 어떠한 확률 분포도 명시하지 않는다는 것을 알아야 합니다. z(G가 input으로 받는 Noise)의 확률 분포가 특정 확률 분포를 따라야 한다는 가정이 없어도 된다는 것입니다. 즉, GAN 방식에서의 generative model은 (z의 확률분포가 무엇인지와는 별개로) 스스로 이미지 데이터의 확률 분포를 estimation할 수 있다는 의미입니다. 결국은 uniform sampling을 하건 gaussaian sampling을 하건 상관없기 때문에 tractable 하다는 것입니다.

4-2. Adversarial net의 목적함수

아래 수식은 Adversarial net의 목적 함수입니다. D는 실제 데이터와 생성된 데이터에 대해 적절한 label을 할당하도록 하는 확률을 최대화하며, log(1-D(G(z)))를 최소화 하도록 G를 동시에 훈련시킵니다.

먼저 D 관점에서 목적 함수를 해석해 보겠습니다.

G를 멈춰 놓고 D를 업데이트 하는 것이라고 이해하시면 될 것 같습니다. G가 생성한 가짜 데이터가 들어오면 0을 출력하고 실제 데이터가 들어오면 1을 출력해야 합니다. 따라서 목적함수의 각 항이 0의 값이 되도록 만들어야 하고, V(D,G)를 최대화하는 값은 0이 됩니다.

다음으로는 G 관점에서 목적 함수를 해석해 보겠습니다.

D를 멈춰두고 G를 업데이트 하는 것이라고 이해하시면 되며, G의 관점에서 Gradient를 계산하게 되면 좌측의 식은 고려할 대상이 아니게 되는 것입니다. 또한 D가 샘플이 실제 데이터 분포에서 나온 것으로 판단하게 만들어야 하기 때문에 D(G(z))의 값이 1이 되도록 만들어야 합니다. 즉, V(D,G)가 음의 무한대 값(-∞)으로 수렴하도록 해야 한다는 것입니다.

학습시키는 과정에서 inner loop에서 를 최적화하는 것은 계산량이 많고 유한한 데이터 셋에서는 overfitting을 초래합니다. 따라서, D의 가중치 계산을 줄이기 위해 D를 최적화하는 k step과 G를 최적화하는 1 step을 번갈아 수행합니다. 이를 통해 D는 최적화 되었고, 따라서 G도 천천히 업데이트 됩니다.

다만 Log(1-D(G(z))를 minimization하기에는 초기에는 D(G(z)) = 0이므로 log(1-(D(G(z))))꼴의 함수에서 초기 D(G(z)) 값이 0이라면 gradient 값 자체가 saturation 된 상태이기 때문에 업데이트가 더디기 때문에 G를 학습시키는 관점을 log(1-(D(G(z))))을 minimization 하는 방향이 아닌, log(D(G(z)))를 maximization하는 방향으로 학습한다고 보시면 됩니다. 밑에 그림을 보시면 D(G(z)) = 0일 때의 기울기가 maximization하였을 때 더욱 가파른 것을 보실 수 있을 것입니다.

위와 같은 이유로 인해 실제 학습에 쓰이는 Value function(=V(D,G))는 아래와 같이 변경됩니다.

4-3.Adversarial net 학습의 진행 과정

이번 섹션에서는 Figure 1에 대해 설명하도록 하겠습니다. 다음은 Figure 1에 이미지를 표현할 수 있는 저차원 latent space를 z차원으로 간주하고, z차원에서 sampling할 때 사전확률 분포를 uniform distribution z~ pz(z)으로 설정하면 일정한 간격으로 sampling하며, 추출된 각각의 sample들로부터 generated image가 생성됩니다.

실제로 z축의 차원과 x축의 차원은 다르기 때문에 1차원 개념으로 표현하면 엄밀히 따지자면 잘못된 것이지만 이해를 돕기 위해 이렇게 표현 한 것으로 보입니다.

위에서 설명한 내용을 아래의 그림과 같이 표현 할 수 있을 것 같습니다.

아래 그림에서는 이미지 같은 데이터가 non-uniform distribution으로 표현 될 수 있음을 언급합니다. 여기서 포인트는 이미지 데이터의 차원에서 이미지 데이터들의 분포를 표현할 때는 uniform distribution으로 표현하기 어렵다는 것입니다. 그래서 정규분포가 아닌 다른 non-uniform distribution으로 볼 수 있습니다.

다음으로는 (a),(b),(c),(d)에 대한 설명을 하겠습니다.

D가 모델링하는 조건부 확률 분포 : 파란색 점선

G가 모델링하는 생성 분포(Pg) : 녹색 실선

실제 데이터 생성 분포(Px) : 검은 점선

하단의 수평선 : z가 균일하게 샘플링되는 도메인

상단의 수평선 : x의 도메인

위로 향하는 화살표 : x=G(z)의 매핑을 통과한 샘플들이 어떤식으로 non-uniform한 p_g​를 나타내도록 하는지 보여줌

(a) data distribution과 generative distribution이 어느정도 유사한 상태-> 아직까지는 잘 구분해주긴 하나, 불안정한 상태

(b) D가 잘 학습이 된 상태 -> (b) 그림상 해당 지점에서 왼쪽 값이면 real data로 구분, 오른쪽 값이면 fake data로 구분 -> D 분포(관점)에서 x축 상의 값이 왼쪽일 수록 fake 이미지라고 판단할 확률(y값)이 높아짐

(c) G를 업데이트 한 후, 학습이 잘 된 D분포의 gradient가 G(z)가 좀 더 의미 있는 이미지를 생성할 수 있게 유도 함 -> 학습이 잘 된 D로 인해 pg(G) 분포가 업데이트 되면서 점점 px분포에 가까워짐

(d) G와 D가 충분히 학습되면 결국, G의 성능이 매우 높아져 D가 real data와 fake data를 전혀 구분하지 못함 -> ½ uniform distribution이 형성 됨

5. Theoretical Results

GAN 논문에서는 딥러닝 모델을 확률 모델로써 설계할 때 크게 네가지 기준으로 요약하고 있습니다.

1. 설계한 확률(딥러닝) 모델이 tractable 한 것인가?
2. 설계한 확률(딥러닝) 모델이 최적해(global optimum)를 갖는가?
3. 설계한 확률(딥러닝) 모델이 최적해(global optimum)에 수렴하는가?
4. 설계한 확률(딥러닝) 모델이 최적해(global optimum)을 찾을 수 있는 알고리즘이 존재하는가?

첫 번째 질문인 tractable 한 것인가는 앞선 Adversarial nets 부분에서 설명하였으며,

나머지 질문들은 Theoretical Results를 리뷰하면서 설명해보겠습니다.

5-1. Global optimality of Pg = Pdata(설계한 확률(딥러닝) 모델이 최적해(global optimum)를 갖는가?)

Generator 관점에서 minmax problem은 pg = pdata에서 global optimum 값을 가져야 합니다. 직관적으로 봤을 때, Generator가 Data와 유사한 distribution을 형성하는 지점인 곳에서 global optimum 값을 찾게 되면 학습이 중단될 것입니다. 이 논문에서는 optimal discriminator의 global optimum값은 아래와 같은 수식에 의해 도출 된다고 합니다.

위 수식의 직관적인 설명은 아래와 같습니다.

Pg = Pdata 일 경우 D*(x) = ½ 값을 갖는데, 이것이 의미하는 바는 discriminator가 가짜 이미지와 진짜 이미지를 판별할 확률이 모두 ½라는 사실과 값습니다. 즉, 가짜와 진짜를 완벽히 혼동한 상태인 것이죠. 그러므로, GAN loss function인 V(D,G) 값이 ½에 가까이 도달하면 학습을 종료하면 됩니다.

아래는 수식의 유도 과정입니다.

D*(x) 값을 원래의 목적 함수에 대입하여 정리하면 아래와 같이 유도 되며

정리하자면, 앞서 언급했던 질문인 “설계한 확률(딥러닝) 모델이 최적해(global optimum)를 갖는가?”에 대해서 “최적해(globaloptimum)”을 갖는다고 할 수 있습니다. MinMax 구조의 함수에서 Pg = Pdata일 때, global optimum을 갖는다고 할 수 있습니다.

5-2. Convergence of Algorithm1(설계한 확률(딥러닝) 모델이 최적해(global optimum)에 수렴하는가?)

딥러닝 모델의 solution을 찾을 수 있는 조건 중 하나가 loss가 convex function인지 확인하는 것입니다. 그래야만 gradient descent와 같은 interative optimization 방식을 통해 해를 찾을 수 있기 때문입니다.

그렇다면 설계한 확률(딥러닝) 모델이 최적해(global optimum)에 수렴하는가?의 질문은 Pg 관점에서 loss 함수가 global optimum으로 수렴할 수 있는지를 확인하면 되는 것입니다. 이를 위해서는 ‘D를 고정시키고, loss 함수가 convex한지 확인하는 것’입니다.

아래 그림을 보시면 D는 고정했기 때문에 U(Pg, D)를 Pg 관점에서 보면 D는 (고정된) 상수값입니다. Pg 관점에서 보면 U(Pg, D)의 변수는 Pg인 셈인 것입니다. 결국, Pg가 학습함에 따라서 변할텐데, 변하는 Pg에 따라서 U(Pg, D)가 convex한지 알아봐야 interative optimization(gradient descent) 방식으로 global optimum을 찾을 수 있는지 확인 할 수 있습니다.

5-3. Algorithm1(설계한 확률(딥러닝) 모델이 최적해(global optimum)을 찾을 수 있는 알고리즘이 존재하는가?)(github 참조)

class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()

        self.linear1 = nn.Linear(img_size, hidden_size2)
        self.linear2 = nn.Linear(hidden_size2, hidden_size1)
        self.linear3 = nn.Linear(hidden_size1, 1)
        self.leaky_relu = nn.LeakyReLU(0.2)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.leaky_relu(self.linear1(x))
        x = self.leaky_relu(self.linear2(x))
        x = self.linear3(x)
        x = self.sigmoid(x)
        return x

Discriminator는 위와 같이 정의할 수 있습니다. 일반적인 multi layer neural network로 구성되어 있습니다. 총 3개의 Linear layer로 구성되어 있으며, 첫번째 layer에서는 MNIST 이미지 사이즈 (1 x 28 x 28 = 784)을 입력받고, 마지막 레이어에서는 classification을 위해 1개의 노드로 정리됩니다.. 각 레이어 사이에는 activation function으로 leaky ReLU 함수가 사용되었으며, 마지막에는 확류로 표현하기 위해 sigmoid 함수가 사용되었습니다.

class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()

        self.linear1 = nn.Linear(noise_size, hidden_size1)
        self.linear2 = nn.Linear(hidden_size1, hidden_size2)
        self.linear3 = nn.Linear(hidden_size2, img_size)
        self.relu = nn.ReLU()
        self.tanh = nn.Tanh()

    def forward(self, x):
        x = self.relu(self.linear1(x))
        x = self.relu(self.linear2(x))
        x = self.linear3(x)
        x = self.tanh(x)
        return x

Generator는 Discriminator와 반대로 구성되어 있습니다. 총 3개의 Linear layer로 구성되어 있으며, 입력값으로 noise vector ‘z’의 크기만큼의 노드가 사용되고, 마지막 layer에서는 실제 MNIST 데이터의 크기 (1 x 28 x 28 = 784) 개의 노드로 정리되었습니다. 각 layer 사이에는 activation function으로 ReLU 함수가 사용되었으며, 마지막 layer 에는 tanh 함수가 사용되었습니다.

criterion = nn.BCELoss()
d_optimizer = torch.optim.Adam(discriminator.parameters(), lr=learning_rate)
g_optimizer = torch.optim.Adam(generator.parameters(), lr=learning_rate)

학습에 사용될 Loss function으로는 BCELoss를 사용하였으며, 국민 optimizor인 Adam을 사용하였습니다.이때, genrator와 discriminator는 서로 따로따로 학습되므로 각각 optimizer를 구분지어 정의해주어야 합니다.

for epoch in range(num_epoch):
    for i, (images, label) in enumerate(data_loader):

        # 라벨을 만들어 줍니다. 1 for real, 0 for fake
        real_label = 
        	torch.full((batch_size, 1), 1, dtype=torch.float32).to(device)
        fake_label = 
        	torch.full((batch_size, 1), 0, dtype=torch.float32).to(device)

        # MNIST dataset의 데이터를 flatten 하게 reshape 해줍니다.
        real_images = images.reshape(batch_size, -1).to(device)

이제 for문을 통해 각 epoch 마다 학습을 시켜주게 됩니다. 학습을 위해 [batch size, 1] 크기의 모두 1로 구성된 real label 의 tensor와 모두 0으로 구성된 fake label의 tensor를 만들어 주었습니다. 또한 [1 x 28 x 28] 크기의 MNIST 데이터를 [batch size, 784] 의 크기로 flatten 해주는 과정을 거쳤습니다.

        # +---------------------+
        # |   train Generator   |
        # +---------------------+

        # Initialize grad
        g_optimizer.zero_grad()
        d_optimizer.zero_grad()

        # fake image를 generator와 noize vector 'z' 를 통해 만들어주기
        z = torch.randn(batch_size, noise_size).to(device)
        fake_images = generator(z)

        # loss function에 fake image와 real label을 넘겨주기
        # 만약 generator가 discriminator를 속이면, g_loss가 줄어든다.
        g_loss = criterion(discriminator(fake_images), real_label)

        # backpropagation를 통해 generator 학습
        g_loss.backward()
        g_optimizer.step()

Generator를 학습시켜 줍니다. Discriminator 를 먼저 학습시키든 Generator를 먼저 학습시키든 상관없지만, 중요한 것은 각자 따로따로 학습시켜줘야 한다는 점입니다. 우선 noise vector ‘z’ 를 torch.randn 함수를 통해 랜덤한 값으로 채워줍니다. 이후 앞서 선언한 generator에 z를 넣어줌으로써 [28 x 28 = 784] 크기의 이미지 데이터를 생성하게 됩니다. 즉 G(z)는 Generator가 생성한 batch size 개수만큼의 이미지가 됩니다. 앞서 설명했듯이 Generator는 D(G(z))의 성능을 낮추는 방향으로 학습되며, loss 함수에 D(G(z))와 real label을 함께 넣어줍니다. Discriminator가 제대로 판단을 할 경우(fake라 판단) Generator는 올바른 방향으로 데이터를 생성하지 못했다고 생각하게 되고, Discriminator 가 제대로 판단하지 못할 경우(real로 판단) Generator는 올바른 방향으로 데이터를 생성했다고 생각하게 됩니다.

	# +---------------------+
        # | train Discriminator |
        # +---------------------+

        # Initialize grad
        d_optimizer.zero_grad()
        g_optimizer.zero_grad()

        # generator와 noise vector 'z'로 fake image 생성
        z = torch.randn(batch_size, noise_size).to(device)
        fake_images = generator(z)

        # fake image와 fake label, real image와 real label을 넘겨 loss 계산
        fake_loss = criterion(discriminator(fake_images), fake_label)
        real_loss = criterion(discriminator(real_images), real_label)
        d_loss = (fake_loss + real_loss) / 2

        # backpropagation을 통해 discriminator 학습
        # 이 부분에서는 generator는 학습시키지 않음
        d_loss.backward()
        d_optimizer.step()

다음으로 Discriminator를 학습시킵니다. 우선 z를 generator에 통과시켜 fake image를 만들어 줍니다. D(G(z)) 값을 loss function에 fake label과 함께 넣어 fake loss를 구해주고, D(x) 값을 loss function에 real label과 함게 넣어 real loss를 구해줍니다. 이렇게 구한 두 fake / real loss를 평균내서 전체 discriminator 의 loss값을 구해줍니다. 이렇게 하면 Discriminator가 제대로 fake 와 real 이미지를 판단할 수 있는 방향으로 학습이 진행되게 됩니다. 이런 과정을 통해 Generator의 성능이 높아지는 방향으로 학습이 진행되게 됩니다.

처음에는 generator가 터무니 없는 데이터를 생성하기 때문에 discriminator가 어렵지 않게 이를 분류할 수 있습니다. 그래서 d_loss 값은 작게 나오고, g_loss값은 크게 나옵니다. 하지만 학습이 진행될수록 d_loss값은 커지고 g_loss값은 점점 작아지는 것을 확인할 수 있습니다. 이는 Discriminator가 점점 진짜와 가짜 이미지를 판단하기 어려워지고, Generator가 점점 진짜같은 가짜 이미지를 생성해낸다는 뜻입니다. 즉, GAN의 기존 의도에 맞게 학습이 되어간다는 뜻입니다. 실제 코드를 돌려보면 알 수 있겠지만, 대략 200 epoch 정도만 학습해줘도 아래 그림과 같이 그럴듯한 데이터가 생성되는 것을 확인할 수 있습니다.

정리해보면 설계한 확률(딥러닝) 모델이 최적해(global optimum)을 찾을 수 있는 알고리즘이 존재하는가?에 대한 답은 알고리즘이 존재한다고 볼 수 있습니다.

6. Experiments

1. MNIST, TFD, CIFAR-10에 대해 훈련
2. generator net는 rectifier linear activation와 시그모이드를 혼합하여 사용
3. discriminator 훈련시 드롭아웃을 사용하고 maxout activation을 사용
4. 이론적 프레임워크에서는 generator의 중간층에 드롭아웃과 노이즈를 허용하지 않지만, 실험에서는 맨 하위 계층에 노이즈 input을 사용

Gaussian Parzen window를 G에 의해 생성된 샘플들에 fitting하고 이렇게 추정된 분포 하에 얻어진 log-likelihood를 확인함으로써 Pg에 대해서 test set 데이터의 확률을 추정하였습니다. 해당 방법을 옳은 평가 척도라고 할 수 없지만 이전 모델과 비교했을 때, 경쟁력을 갖추고 있고, 잠재력을 보여줍니다.

아래 수식을 이용하면 실제 이미지 데이터에 대응하는 z 값을 찾을 수 있습니다.

이렇게 찾은 z값들 간에 vector linear interpolation을 하게 되면, 7과 1사이의 z 중간 값이 9가 나오는걸 확인할 수 있습니다.

7. Advantages and Disadvantages

7-1. Advantages

1. backpropagation으로 gradient를 구할 수 있기 때문에 Markov chain이 필요하지 않음
2. 학습 과정에 inference를 할 필요가 없음
3. adversarial nets framework와 다양한 함수 병합 가능
4. generator network가 실제 데이터로부터 직접적으로 업데이트되지 않고 discriminator로부터 흘러들어오는 gradient만을 이용해 학습될 수 있어 통계적 이점을 가져옴

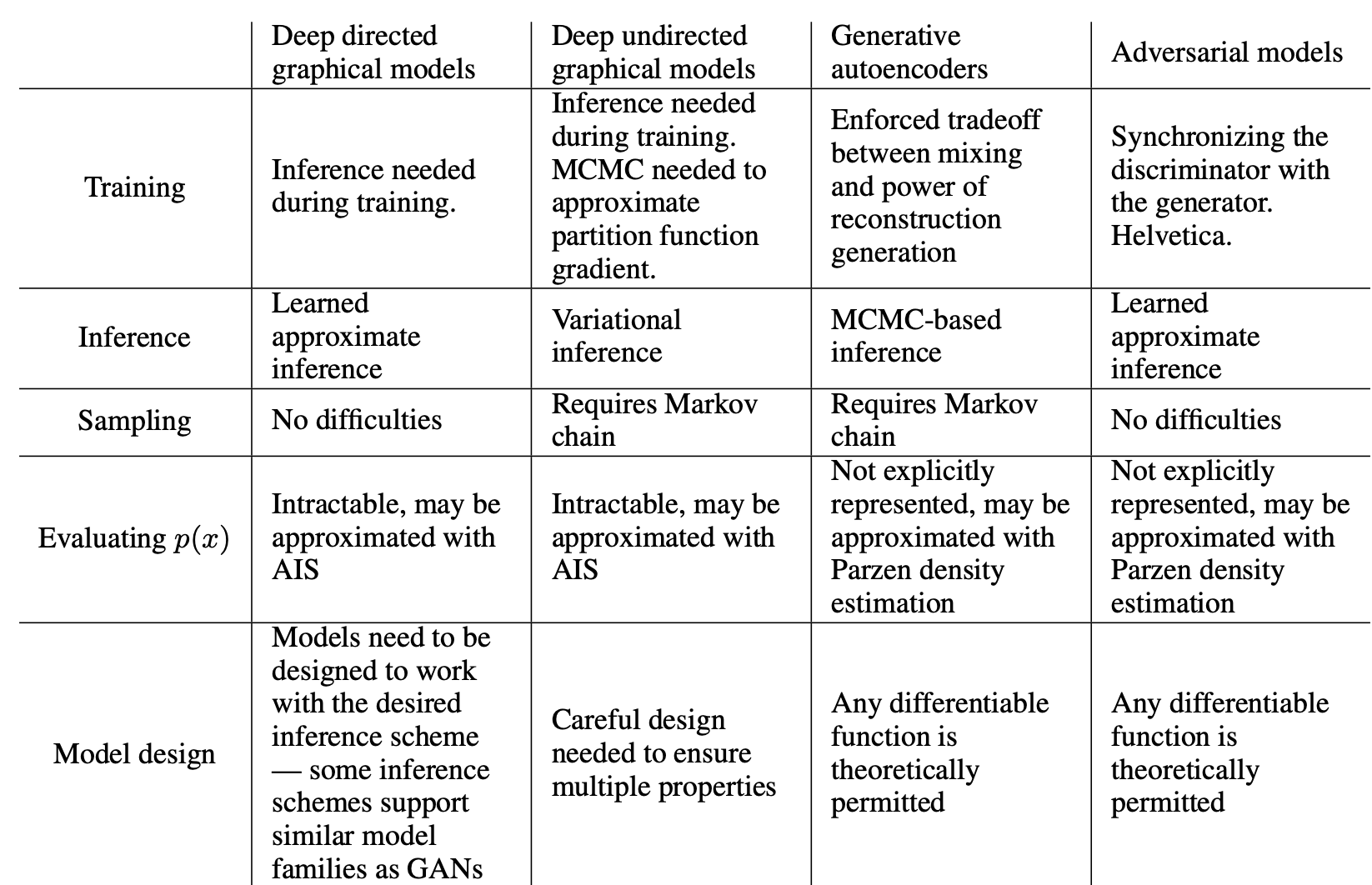
아래의 표를 통해 다른 모델들과의 차이점을 정리하였습니다.

7-2. Disadvantages(Mode collapse)

GAN은 Mode collapse가 일어날 수 있다는 한계점이 존재합니다. 아래 그림을 보시면 3개의 검은 실선이 실제 이미지를 나타내며, 각각의 실선들을 mode라고 부르며(representation할 목표) 금발 여성, 흑발과 안경을 쓰고 있는 남성, 흑발 여성을 나타내며, 원하는 목표는 실선 3개를 모두 표현해줄 수 있는 확률 분포를 익히는 것으로 볼 수 있습니다. 가운데 실선에 해당하는 데이터 셋이 제일 많다고 한다면, VAE는 제일 데이터 셋이 많은 그룹에 맞게 distribution을 형성하면서 동시에 normal distribution을 이용해 주변 이미지 그룹들도 다 포괄할 수 있도록 학습을 하기 때문에 모든 데이터 그룹을 포괄하려는 것을 볼 수 있습니다. 반대로 GAN은 generator가 만드는 이미지 그룹을 discriminator가 더 이상 구별해내지 못할 때, real image가 들어왔을 때 맞출 확률이 ½이거나 fake image가 들어 왔을 때 맞출 확률이 ½이 되면 학습이 종료가 됩니다. 그렇기 때문에 이미지 데이터 셋이 많은 가운데 실선에 해당하는 그룹만 학습하다 끝내버리면 해당 그룹만 잘 generation해주는 현상이 발생 할 수 있습니다. 각각의 실선이 우리가 representation 해야할 중요한 mode라고 부르며, GAN에서는 이러한 mode들을 잘 학습하는 것이 안되는 collapsing 현상이 일어난다는 단점을 가지고 있습니다.

8.Conclusion and future work

8-1. GAN의 한계점 보완 연구

1. Simple Example : Minimax 최적화 문제를 해결하는 과정이기 때문에, oscillation이 발생하여 모델이 불안정(두 모델의 성능 차이로 bias되는 문제를 DCGAN으로 개선)
2. 학습 데이터의 분포를 따라가기 때문에 어떤 데이터가 생성될지 예측하기 어려움(cGAN(Conditional GAN)을 이용하여 문제 개선)
3. overfitting : 수동 튜닝을 안하고 과정합정도에 따라 동적으로 제어하는 Adaptive discriminator augmentation mechanism 방식 활용 (Training Generative Adversarial Networks with Limited Data, 2020 참조)
   
   

Reference

Original paper : Generative Adversarial Networks

[1] Conditional Generative Adversarial Nets, Mehdi Mirza, Simon Osindero (2014)

[2] Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, Alec Radford, Luke Metz, Soumith Chintala (2016)

[3] Auto-Encoding Variational Bayes, Diederik P Kingma, Max Welling (2014)

[4] Stochastic Backpropagation and Approximate Inference in DGM, Rezende, Danilo Jimenez; Mohamed, Shakir; Wierstra, Daan. ICML (2014)

[5] Training Generative Adversarial Networks with Limited Data, Tero Karras, Miika Aittala, Janne Hellsten, Samuli Laine, Jaakko Lehtinen, Timo Aila (2020)

[6] 1시간만에 GAN(Generative Adversarial Network) 완전 정복하기

[7] [논문 정리] GAN에 대해서 알아보자

[8] 초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets

[9] 5-1. GAN (Part1. GAN architecture)

[10] github 소스 코드