PGGAN

https://arxiv.org/abs/1710.10196

Contribution

논문의 contribution은 크게 2가지다.

고품질 고해상도 이미지를 생성하면서 안정적으로 학습이 가능한 모델을 제안한다
GAN이 생성하는 이미지를 평가하고 비교하기 위한 새로운 평가지표를 제안한다.

Background

GAN

Generative Adversarial Network(GAN)은 2014년 몬트리올 대학의 연구진이 제안한 신경망 구조이다. GAN은 실제와 매우 유사한 이미지, 영상, 오디오 등의 데이터를 생성하기 위해 만들어 졌다. Generative model중 Variational Autoencoder(VAE)나 Flow Model등 여러 모델들과 함께 가장 활발히 연구되어 지고 있는 분야이다.

GAN

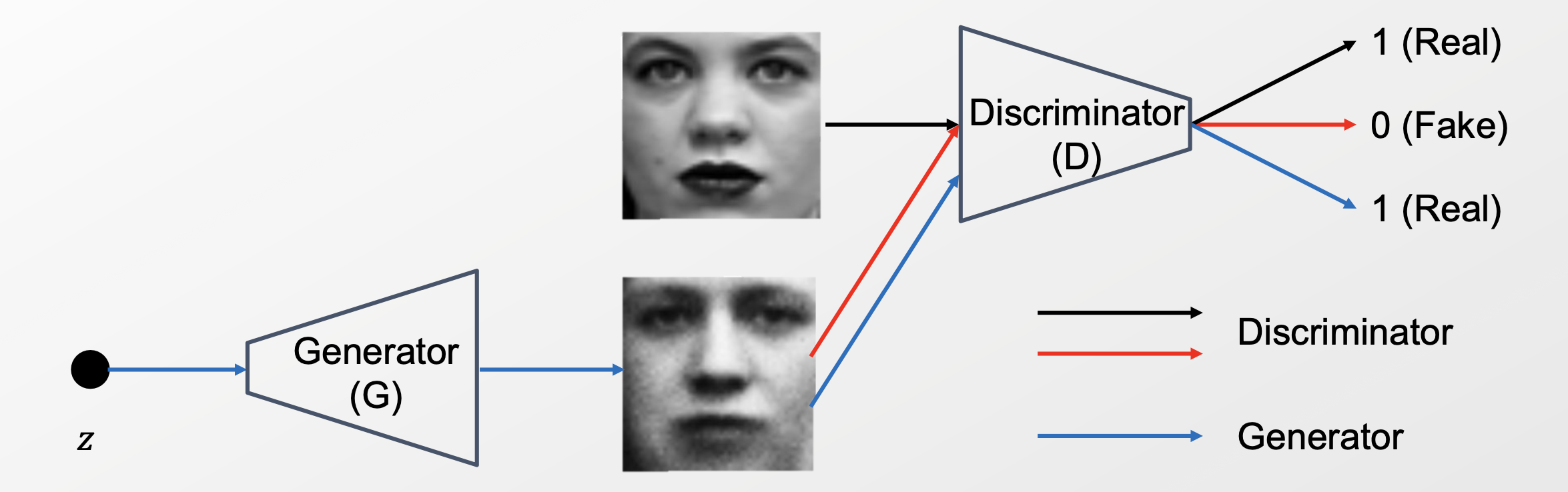
GAN은 위와 같이 Generator와 Discriminator로 구성되어져 있다.

Generator : random한 노이즈를 원래의 데이터와 비슷하도록 변환하는 모델
Discriminator : Discriminator에 들어오는 input 데이터가 generator가 만든 fake data인지, real data인지 구별하도록 하는 모델

GAN은 Generator와 Discriminator가 서로 경쟁하듯 스스로를 학습시켜 나가는 구조를 가지고 있다. 이러한 기본적인 GAN 구조를 기반으로 개선된 다양한 모델들이 연구되고 있으며, 본 논문의 주제인 PGGAN 역시 GAN구조를 기반으로 한다.

Ian J. Goodfellow, Jean Pouget-Abadie∗, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair†, Aaron Courville, Yoshua Bengio‡ Generative Adversarial Nets, 2014.

RMSProp & Adam

RMSProp은 Back Propagation을 위한 gradient를 계산할 때 지수 가중 이동 평균(Exponentially weighted moving average)을 이용하여 최신의 기울기들이 더 크게 반영되도록 하는 방법이다. RMSProp의 식은 다음과 같다. $ L(\theta_{k}) $ 는 가중치 $\theta_{k}$ 가 주어졌을 때의 loss값이다. $\eta$ 는 learning rate다.

\[\begin{align} &s_{k} \leftarrow \beta s_{k-1} + (1-\beta)(\nabla_{\theta} L(\theta_{k}))^{2} \\ &\theta_{k+1} = \theta_{k} - \alpha \frac{\eta}{\sqrt{s_{k}}}\nabla_{\theta} L(\theta_{k}) \end{align}\]

Adam은 Momentum과 RMSProp을 조합하여 구성한 방법이다. Adam의 식은 다음과 같다.

\[\begin{align} m_{k} &= (1-\beta_{1})\nabla_{\theta} L(\theta_{k})+\beta_{1} m_{k-1} \\ v_{k} &= (1-\beta_{2})\nabla_{\theta} L(\theta_{k})^{2}+\beta_{2} v_{k-1} \\ \hat{m_{k}} &= \frac{m_{k} }{ 1-\beta_{1}^{k}} \\ \hat{v_{k}} &= \frac{v_{k} }{ 1-\beta_{2}^{k}} \\ \theta_{k+1} &= \theta_{k} - \alpha \frac{\eta }{\sqrt{\hat{v_{k}}}+\epsilon}\hat{m_{k}} \end{align}\]

두 방법의 공통점은 마지막에 magnitude(standard deviation)으로 나눠 주어 스케일이 normalize되어 있다는 것이다. 본 논문에서도 이와 같은 아이디어를 사용하고, 같은 목적을 달성하기 위하여 He’s initializer 방법을 사용하였다.

Sebastian Ruder, An overview of gradient descent optimization algorithms∗, 2017.

He’s initializer

Initialization은 activation들이 합리적인 scale을 가지게 해서 계속 증가하거나 감소하는 것을 방지하기 위한 방법이다. 합리적인 activation이란 일반적으로 standard deviation이 1인 경우가 된다. 이 조건을 맞춰주기 위해 Xavier initializer가 제안되었으며, 이후에 He’s initializer는 Xavier initializer 방법에서 activation function이 ReLU라고 가정하여 initialization해주는 방법이다. initialization 식은 아래와 같다.

\[W_{i} \sim N(0, \frac{1 }{ \sqrt{\frac{1 }{ 2} D_{a}}})\]

식에서 보면 normalization constant 는

\[\frac{1}{\sqrt{\frac{1}{2} D_{a}}}\]

이다.

Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, 2015.

Ms-ssim

사람의 인지(perceptual)를 바탕으로 이미지 유사성을 판단하려는 몇몇 metric중에 MS-SSIM는 가장 많이 사용되고 있는 것 중 하나이다. MS-SSIM은 SSIM을 0.0~1.0으로 scaling한 것으로, 1.0에 가까울 수록(값이 더 높을 수록) 더 유사한 이미지라고 판단한다.
본 논문에서는 새로운 metric을 제안하는데 MS-SSIM과 비교하여 제안된 metric의 장점을 소개하고 있다.

Z. Wang, E. P. Simoncelli, and A. C. Bovik. Multiscale structural similarity for image quality assessment. In Signals, Systems and Computers, 2004. Conference Record of the Thirty-Seventh Asilomar Conference on, pages 1398–1402 Vol.2, 2004.

WGAN & WGAN-GP

Wasserstein GAN(WGAN)은 기존의 DCGAN 구조를 바탕으로, 향상된 metric을 제안하였다. 이 metric이 Wasserstein distance이다.

\[W(P_{r}, P_{\theta}) = \sup_{\Vert D \Vert_{L} \leq 1} E_{x \sim P_{r}} [D(x)] - E_{\tilde{x} \sim P_{g}} [D(\tilde{x})]\]

이 방법으로 기존의 GAN보다는 더 안정적으로 학습할 수 있었지만, 여전히 좋지 않은 샘플들을 만들거나 수렴하지 못하는 문제가 발생하였다. [WGAN-GP 논문]에서는 WGAN에서 사용하는 weight clipping이 문제의 원인이라고 보고, weight clipping대신 ‘Gradient Penaty’방법을 제안하여 해결하였다. WGAN-GP Loss-function의 식은 아래와 같다.

\[L = E_{\tilde{x} \sim P_{g}} [D(\tilde{x})] - E_{x \sim P_{r}} [D(x)] + \lambda E_{\hat{x} \sim P_{\hat{x}}}[(\Vert \nabla_{\hat{x}} D(\hat{x}) \Vert_{2} - 1)^{2}]\]

본 논문에서는 가장 좋은 성능을 보이는(state-of-art) WGAN-GP Loss-function을 사용하였다.

WGAN : Martin Arjovsky, Soumith Chintala, L´eon Bottou, Wasserstein GAN, 2017.

WGAN-GP : Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, Aaron Courville, Improved Training of Wasserstein GANs,2017. https://dl-ai.blogspot.com/2017/08/gan-problems.html

problem

GAN에 있는 challenge는 다음과 같다.

mode collapse : generator가 같은 이미지만 생성한다.
불안정한 학습: discriminator가 overshoot되면서 unhealthy competition 이 발생한다.
High-resolution image는 생성하도록 학습시키는 것은 더욱 불안정하다. → discriminator가 overshoot되기 쉽다.

proposed method

Low resolution image부터 시작하여 안정적으로 학습시키고 학습이 안정화 되면 해상도를 증가시키고 학습시킨다. 이를 통해 고해상도 이미지 생성모델을 빠르고 안정적으로 학습시킬 수 있을 것이다.

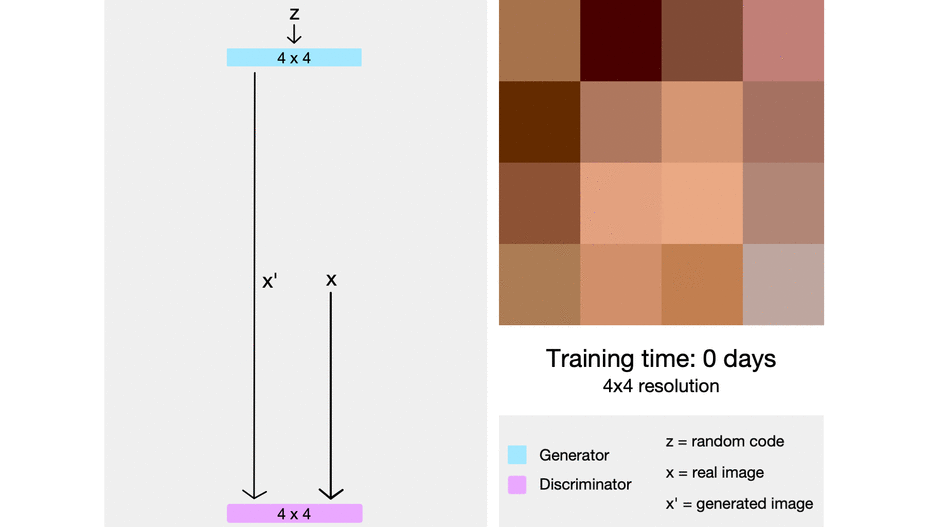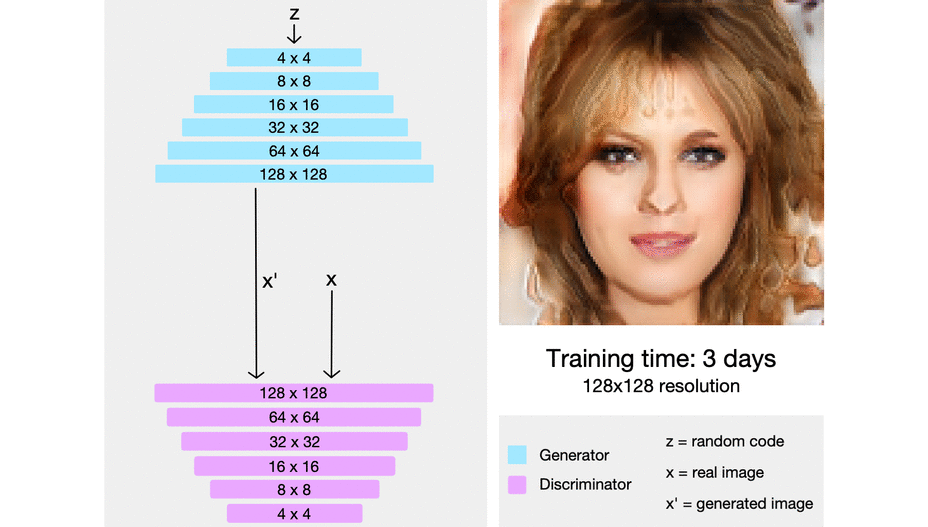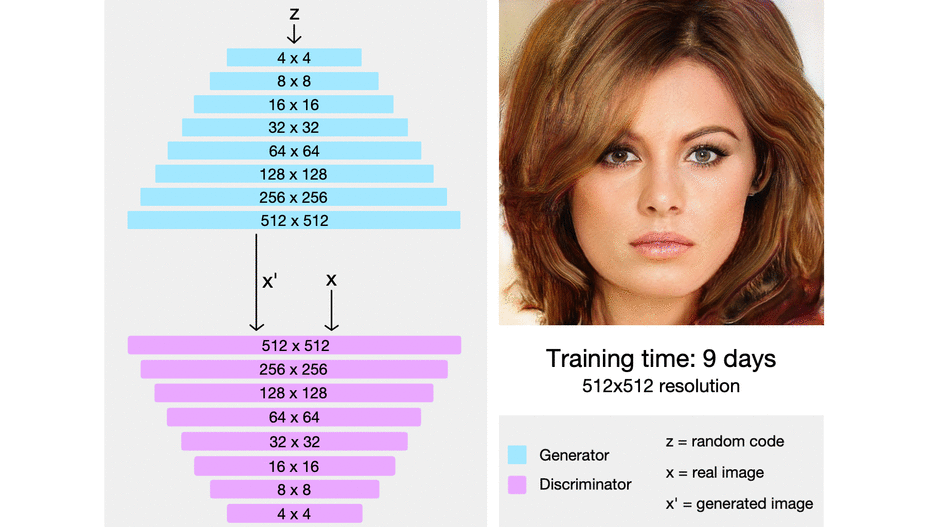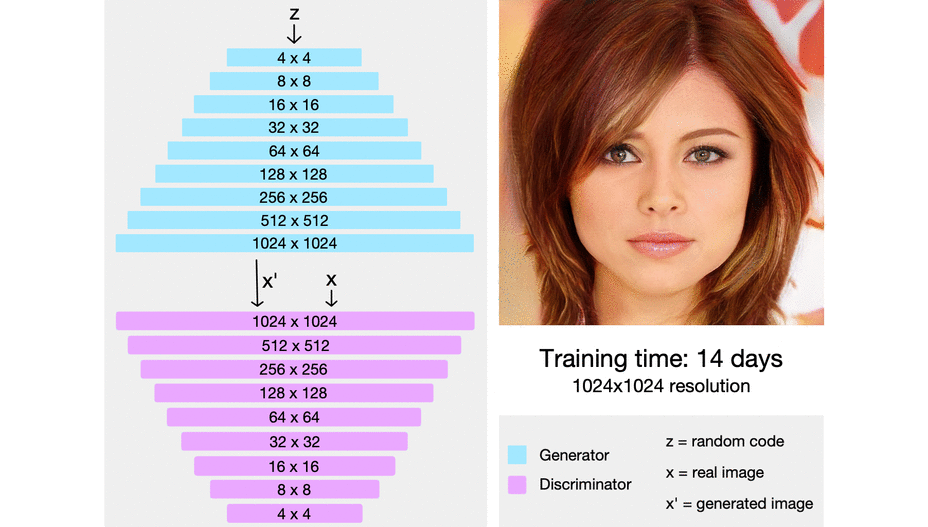
https://towardsdatascience.com/progan-how-nvidia-generated-images-of-unprecedented-quality-51c98ec2cbd2

논문에서 해결하는 challenge

새로운 층을 추가했을때 모델에 가해지는 충격이 한번에 전해지지 않도록 해야한다. 이를 위해 Fade in을 사용하여 추가된 layer의 soft landing을 돕는다.
기존의 GAN loss는 generator의 분포의 다양성을 명시적으로 부여하지 않는다. discriminator에 입력되는 이미지들의 통계정보를 같이 넘겨 discriminator가 이미지 뿐만 아니라 분포도 고려하여 진위여부를 판단하도록 한다.
GAN의 학습이 불안정하다. Pixel Normalization, WGAN-GP loss, Weight Scaling을 적용하여 이러한 문제에 접근한다.
GAN을 평가하기 위한 지표로 MS-SSIM은 한계가 있으며 이를 해결하기 위한 새로운 평가지표를 제안한다.

Progressive Growing of GANs

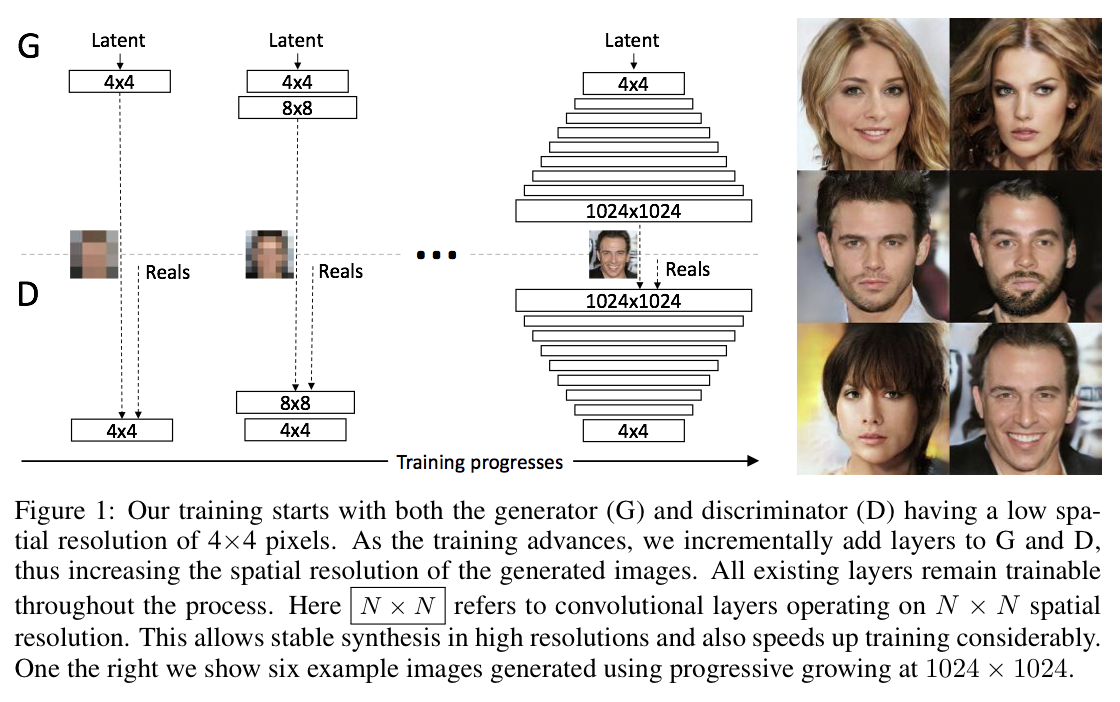
Untitled

핵심 아이디어는 비교적 간단하다. 학습과정에서 단계적으로 해상도를 증가하는 것이다. 이러한 방법을 통해 모델은 latent code에서 High resolution까지의 복잡한 mapping을 한번에 학습하는 것을 단계적으로 접근할 수 있기에 학습이 안정적이고 결론적으로 빠르게 수렴할 것을 기대 할 수 있을 것이다. 이렇게 학습과정에서 모델의 크기를 키우면서 단일 모델로 고해상도 이미지를 생성하도록 한다.

Fade in

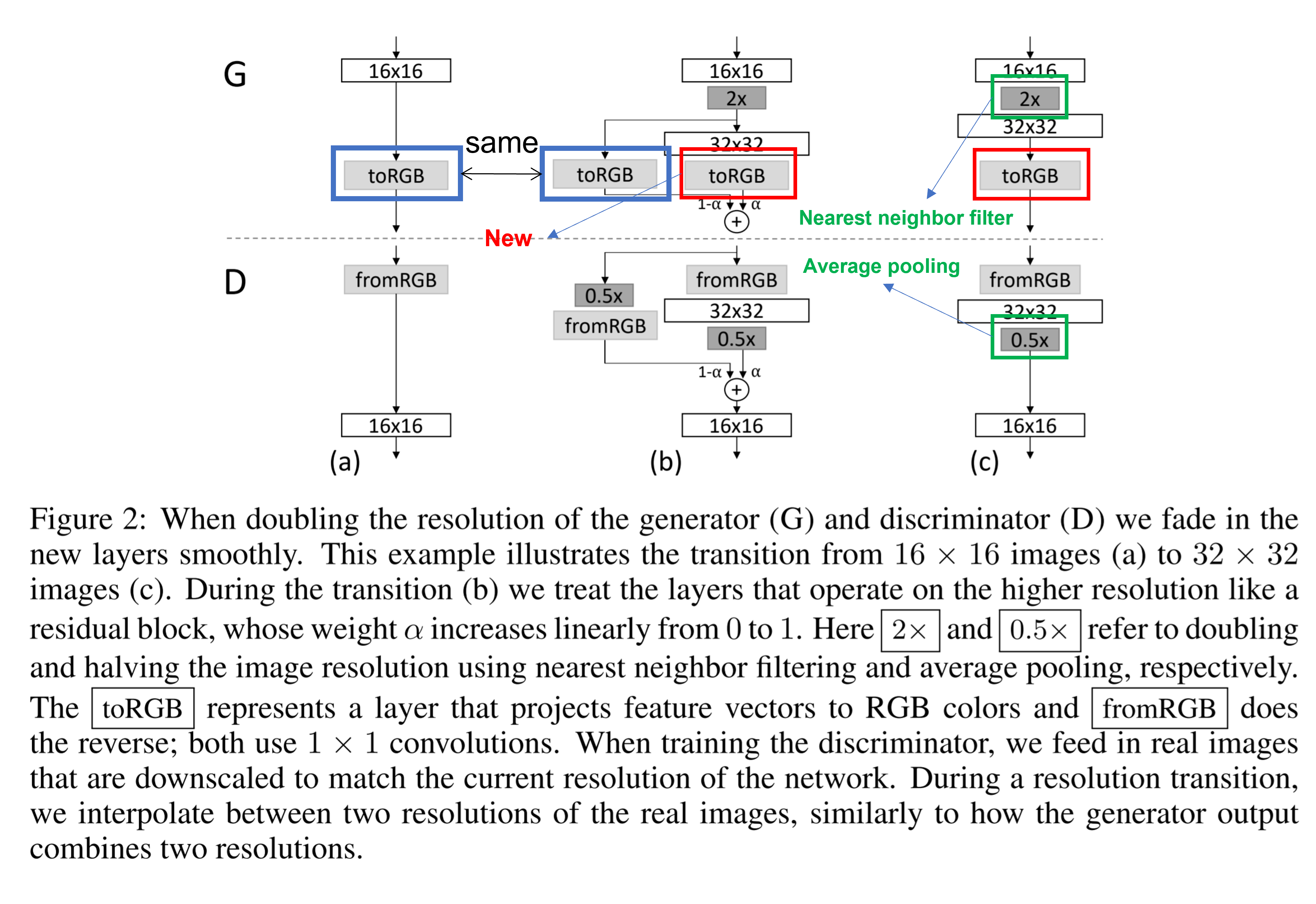
새로운 층을 모델에 올리게 되면 모델 전체에 충격이 가해진다. 이를 방지하기 위해서 $\alpha(0~to~1)$를 사용해서 이전 층과 새로운 층의 결과를 더해 학습이 진행되면서 안정적으로 새로운 층이 정착하도록 돕는다.

figure2의 그림 (a), (b), (c)는 (a) → (b) → (c)의 과정을 통해 16* 16 해상도의 이미지를 생성하도록 학습된 모델이 32*32 해상도의 이미지를 생성하도록 학습하게되는 것을 보여준다.

그림 a에서는 학습이 완료된 모델 Generator: … → 16* 16 layer → 1* 1convolution layer(ToRGB), Discriminiator: 1* 1 convolution(fromRGB) → 16* 16 layer → … 이 있다.

그림 b는 해상도를 두 배로 증가시키는 과정이다. 해상도 증가는 단순한 nearest neighbor filiter와 Average pooling을 이용한다, resolution doubling 후 residual block 구조와 $\alpha$를 사용하여 fadein 을 수행한다. 이때 추가된 convolution layer를 거치지 않는 short path 쪽 toRGB는 학습된 layer를 사용한다. $\alpha$는 0에서 1로 증가한다.

이러한 방식은 새로운 layer가 아예 새로운 것을 학습하는 것이 아니라 간단한 부분을 학습한다. 이전 layer의 출력이 표현하는 large scale structure에 details를 추가하는 것을 학습하는 것이다. 고해상도 layer에서도 large scale structure가 유지되도록 하여 학습이 불안정해지는 것을 방지하는 효과를 갖게된다.

Increasing variation using minibatch standard deviation

GAN은 training dataset의 일부만을 학습하는 경향을 보인다. 이를 해결하기위해 minibatch discriminator 가 제안 되었는데 이는 이미지 내에서 뿐만 아니라 minibatch 전체에 걸친 feature statistics를 discriminator에 전달하여 generator가 생성하는 이미지들의 분포도 고려하도록 만든다.

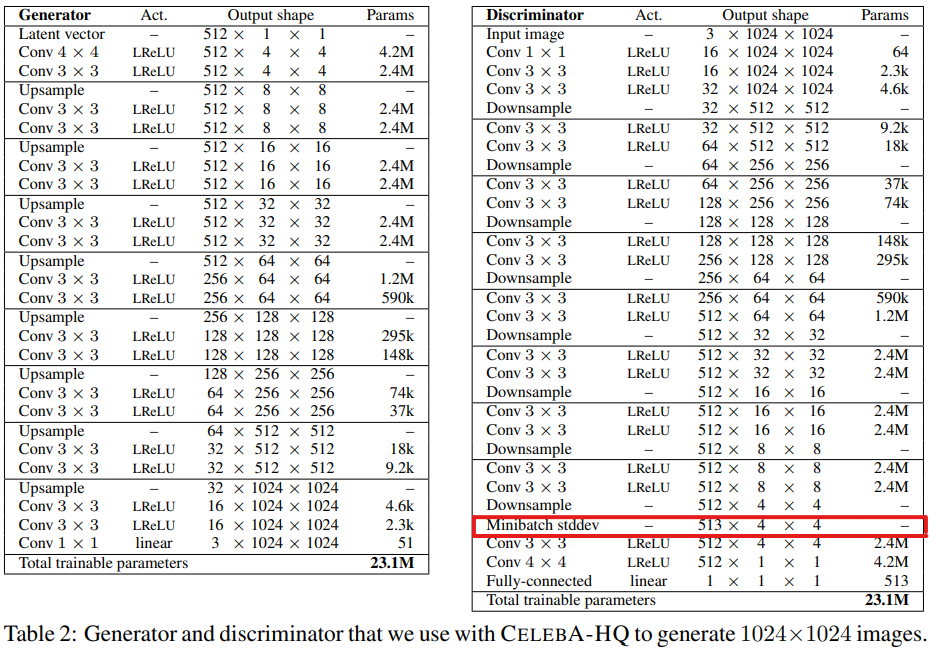
Untitled

기존의 방법은 학습가능한 레이어를 활용하였지만 pggan 에서는 단순히 통계 값만 계산하고 features에 concate하여 이를 간단하게 수행한다.

model collapsing을 방지하기 위해 미니배치 전체에서 feature map들의 표준편차를 feature map들에 concat해서 (예 512* 4* 4 입력이 들어오면 512개의 feature map의 표준편차를 값으로 갖는 4* 4 배열로 만들어 concat해 513* 4* 4의 output을 내보낸다 minibatch에 대한 통계정보를 discriminator에 같이 제공함으로써 variation에 대한 학습효과를 증진시키려는 시도를 했다.

minibatch의 통계정보를 discriminator에 넘겨 통계정보를 real/fake를 구분하는데 사용할수 있게 하였고 이를 통해 generator도 real minibatch와 같은 통계적 특징을 갖도록 fake image를 생성하도록 하는 것이다.

\[MAPs \in \mathbb{R}^{N\times C \times H \times W} \text{ (N feature maps)}\\ \text{Split minibatch into M groups of size G.}\\ \begin{aligned} &Y:=Reshape_{G \times M \times C \times H \times W}(MAPs)\\ &mean_{M \times C \times H \times W}=\frac{1}{G}\sum^{G}_{i=0}Y_{[i,M,C,H,W]}\\ &std_{M \times C \times H \times W} =\sqrt{\frac{1}{G}\sum^{G}_{i=0}(Y_{[i,M,C,H,W]}-mean_{[M,C,H,W]})^2+\epsilon}\\ &AvgStdMAPs_{M \times 1 \times 1 \times 1}=\frac{1}{C*H*W}\sum^{C}_{c=0}\sum^{H}_{h=0}\sum^{W}_{w=0}(std_{c,h,w})\\ &\text{MiniBatch StdDev} := tile_{N \times 1 \times H \times W}(AvgStdMAPs) \end{aligned}\]

#----------------------------------------------------------------------------
# Minibatch standard deviation.

def minibatch_stddev_layer(x, group_size=4):
    with tf.variable_scope('MinibatchStddev'):
        group_size = tf.minimum(group_size, tf.shape(x)[0])     
				# Minibatch must be divisible by (or smaller than) group_size.
        s = x.shape                                             
				# [NCHW]  Input shape.
        y = tf.reshape(x, [group_size, -1, s[1], s[2], s[3]])   
				# [GMCHW] Split minibatch into M groups of size G.
        y = tf.cast(y, tf.float32)                              
				# [GMCHW] Cast to FP32.
        y -= tf.reduce_mean(y, axis=0, keepdims=True)           
				# [GMCHW] Subtract mean over group.
        y = tf.reduce_mean(tf.square(y), axis=0)                
				# [MCHW]  Calc variance over group.
        y = tf.sqrt(y + 1e-8)                                   
				# [MCHW]  Calc stddev over group.
        y = tf.reduce_mean(y, axis=[1,2,3], keepdims=True)      
				# [M111]  Take average over fmaps and pixels.
        y = tf.cast(y, x.dtype)                                 
				# [M111]  Cast back to original data type.
        y = tf.tile(y, [group_size, 1, s[2], s[3]])             
				# [N1HW]  Replicate over group and pixels.
        return tf.concat([x, y], axis=1)                        
				# [NCHW]  Append as new fmap.

normalization in generator and discriminator

GAN의 Generator와 Discriminator의 unhealthy competition의 결과로 escalation of signal magnitudes이 발생하는 경향을 보인다. 대부분의 경우 이러한 상황에서 batch normalization 을 사용하지만 batch normalization은 원래 covariate shift를 막기 위해 나왔다. GAN에서는 이런 문제는 보고 된 적이 없고 실제로 GAN에 필요한 것은escalation of signal magnitudes를 막는 것이다. PGGAN에서는 EQUALIZED LEARNING RATE equalized learning rate와 pixelwise feature vector normalization을 통해 이를 해결하고자 한다.

EQUALIZED LEARNING RATE - Weight Scaling

weight 를 gaussian(0,1)으로 초기화 하고, 다음과 같이 Runtime에 명시적으로 scaling을 해준다. 이때 scale 상수는 He’s initialization에서 제시된 정규화 상수를 사용한다.

\[\hat{w}_i= cw_i\\ c=\sqrt{\frac{2}{n_{in}}}\\ w_i \text{ are weight }\\ n_{in} \text{ is number of previous node}\]

이러한 조치는 모든 layer들 output의 분산이 1이 되도록 한다. 이것은 runtime에서 수행하면 layer parameters의 Dynamic range들이 비슷하도록 한다. 그리고 이렇게 parameter의 Dynamic range가 비슷하면 RMSprop나 ADAM과 같은 표준편차를 추정하여 이것으로 gradient를 normalize하는 gradient descent method와 같이 사용될 때 모든 weights의 learning speed를 동일하게 하는 효과가 있다.

한편, 모든 layer의 output의 평균과 분산이 각각 0,1일 때 deeper layer를 갖는 모델에서 gradient vanishing/exploding을 피할 수 있다고 한다.

\[\mathbb{E}[X_i]=0, Var(X_i)=1 \text{ 일때 }\\ Y=\sum^{n}_{i=1}X_iW_i\\ \begin{aligned} Var(Y)&=\sum^{n}_{i=1}Var(X_iW_i)\\ &=\sum^{n}_{i=1}Var(X_i)Var(W_i)\\ &=\sum^{n}_{i=1}Var(W_i)\\ \end{aligned}\]

즉, Y의 분산이 1이 되기 위해서는 W의 분산이 $\frac{1}{n}$이 되어야 한다. 다만 activation function이 Relu인 경우 W의 분산은 $\frac{2}{n}$이어야 한다.

# Get/create weight tensor for a convolutional or fully-connected layer.

def get_weight(shape, gain=np.sqrt(2), use_wscale=False, fan_in=None):
  if fan_in is None: fan_in = np.prod(shape[:-1])

  std = gain / np.sqrt(fan_in) # He init
  if use_wscale:
      wscale = tf.constant(np.float32(std), name='wscale')
      return tf.get_variable('weight', shape=shape, initializer=tf.initializers.random_normal()) * wscale
  else:
      return tf.get_variable('weight', shape=shape, initializer=tf.initializers.random_normal(0, std))

PIXELWISE FEATURE VECTOR NORMALIZATION IN GENERATOR

generator와 discriminator의 경쟁으로 magnitude가 통제불능 상태가 되는 것을 막기 위해 feature vector를 pixelwise로 normalize 해준다. local response normalization를 변형한 아래와 같은 식을 통해 이를 수행한다. normalization의 여부가 결과물에 안 좋은 영향을 주지는 않지만 magnitude의 증가는 성공적으로 막았다.

\[b_{x,y}=\frac{a_{x,y}}{\sqrt{\frac{1}{N}\sum^{N-1}_{j=0}(a_{x,y}^{j})^2+\epsilon}}\\\text{where }\epsilon=10^{-8},\\N\text{ is the number of feature maps,}\\\]

$a_{x,y}\text{ and }b_{x,y} \text{ are the orginal and normalized feature vector in pixel }(x,y)$

# Pixelwise feature vector normalization.

def pixel_norm(x, epsilon=1e-8):
    with tf.variable_scope('PixelNorm'):
        return x * tf.rsqrt(tf.reduce_mean(tf.square(x), axis=1, keepdims=True) + epsilon)

MULTI-SCALE STATISTICAL SIMILARITY FOR ASSESSING GAN RESULTS

여러 종류의 GAN이 생성한 이미지를 비교하는 것은 어려운 일이다. 사람의 주관이 들어갈 수 있고 많은 이미지를 평가해야하기 때문이다. MS-SSIM의 경우 mode collapes를 잘 찾아내지만 color나 texture의 특징은 잘 잡지 못 한다.

논문에서는 잘 학습된 GAN의 generator가 생성한 이미지들의 local image structure은 다양한 scale에서 훈련 데이터세트의 그것과 비슷할 것이라는 직관을 바탕으로 해서 새로운 평가 방법을 제안한다.

이미지를 laplacian pyramid으로 표현할 때 각 level은 어떤 spatial frequency 대역에 대응시킬 수 있는데 실제 이미지와 생성한 이미지가 laplacian pyramid 표현상 같은 level에서 비슷한 local image structure 분포를 보인다면 생성한 이미지가 실제 이미지와 비슷하다는 직관에 기반한다.

[http://sepwww.stanford.edu/data/media/public/sep/morgan/texturematch/paper_html/node3.html](http://sepwww.stanford.edu/data/media/public/sep/morgan/texturematch/paper_html/node3.html)

http://sepwww.stanford.edu/data/media/public/sep/morgan/texturematch/paper_html/node3.html

1) local descriptors구하기

training set의 이미지 중 무작위로 뽑은 16384개 이미지의 laplacian pyramid들을 만들고 각 level에서 descriptors 128개를 추출하면 level당 $2^{21}$개의 descriptors 를 얻을 수 있다.

\[x \in \mathbb{R}^{7 \times 7 \times3} \quad x \text{ denote descriptor of image}\\\]

하나의 descriptors 는 7* 7에 3 channels를 갖는 matrix이며 각 이미지에서 무작위 뽑은 픽셀 7*7=49개로 이뤄져 있다.

\[\{x^l_i\}^{2^{21}}_{i=1},\{y^l_i\}^{2^{21}}_{i=1} \\ l \text{ denote level}\\y \text{ denote generated image patch, }\\x \text{ denote training image patch}\\\]

def get_descriptors_for_minibatch(minibatch, nhood_size, nhoods_per_image):
    S = minibatch.shape # (minibatch, channel, height, width)
    assert len(S) == 4 and S[1] == 3
    N = nhoods_per_image * S[0]
    H = nhood_size // 2
    nhood, chan, x, y = np.ogrid[0:N, 0:3, -H:H+1, -H:H+1]
    img = nhood // nhoods_per_image
    x = x + np.random.randint(H, S[3] - H, size=(N, 1, 1, 1))
    y = y + np.random.randint(H, S[2] - H, size=(N, 1, 1, 1))
    idx = ((img * S[1] + chan) * S[2] + y) * S[3] + x
    return minibatch.flat[idx]

2) statistical similarity 구하기

local descriptors를 정규화 하고 Sliced Wasserstein Distance(SWD)를 구하면 된다.

def finalize_descriptors(desc):
    if isinstance(desc, list):
        desc = np.concatenate(desc, axis=0)
    assert desc.ndim == 4 # (neighborhood, channel, height, width)
    desc -= np.mean(desc, axis=(0, 2, 3), keepdims=True)
    desc /= np.std(desc, axis=(0, 2, 3), keepdims=True)
    desc = desc.reshape(desc.shape[0], -1)
    return desc

$\text{statistical similarity}:=\text{SWD}({x^l_i},{y^l_i}) \text{ where } {x^l_i},{y^l_i} \text{ is normalized patchs}$

\[\text{SWD}(x,y)=\int_{\theta \in \Omega}W(X_{\theta},Y_{\theta})^2d\theta \quad \text{ where }X_\theta=\{ \langle X_\theta,\theta \rangle \}_{i \in I} \subset \mathbb{R}\\ W(X,Y)=\inf_{\gamma \in \Gamma(X,Y)}\mathbb{E}_{(x,y) \sim \gamma}|x-y| \quad \text{ where }\Gamma(X,Y) \text{ is all couplings of X,Y}\]

실제 이미지와 생성한 이미지의 descriptors를 normalization하고 sliced wasserstein distance를 구하여 값이 작다면 generator가 생성한 이미지가 실제와 비슷하다고 평가 할 수 있다. sliced wasserstein distance를 사용하는 이유는 효율적으로 계산할 수 있기 때문인것 같다.

해당 내용의 코드는 아래와 같다.

def sliced_wasserstein(A, B, dir_repeats, dirs_per_repeat):
    assert A.ndim == 2 and A.shape == B.shape                           
		# (neighborhood, descriptor_component)
    results = []
    for repeat in range(dir_repeats):
        dirs = np.random.randn(A.shape[1], dirs_per_repeat)             
				# (descriptor_component, direction)
        dirs /= np.sqrt(np.sum(np.square(dirs), axis=0, keepdims=True)) 
				# normalize descriptor components for each direction
        dirs = dirs.astype(np.float32)
        projA = np.matmul(A, dirs)                                      
				# (neighborhood, direction)
        projB = np.matmul(B, dirs)
        projA = np.sort(projA, axis=0)                                  
				# sort neighborhood projections for each direction
        projB = np.sort(projB, axis=0)
        dists = np.abs(projA - projB)                                   
				# pointwise wasserstein distances
        results.append(np.mean(dists))                                  
				# average over neighborhoods and directions
    return np.mean(results)                                             
		# average over repeats

직관적으로 Wasserstein distance가 작다는 것은 patch의 분포가 유사하다는 것, 즉 training image와 generated image가 해당 해상도에서 appearance and variation 모두 유사하다는 뜻이다. 가장 낮은 해상도(16*16)에서 추출한 patch set 간의 거리는 이미지 전체 구조의 유사성을 나타내는 반면, 가장 높은 해상도에서 추출한 patch는 pixel 수준에서의 속성에 대한 정보를 인코딩하고 있다고 볼 수 있다.

EXPERIMENTS

실험에서 사용된 모델은 아래와 같고 WGAN-GP loss 또는 LSGAN loss를 사용하였다. 데이터 세트는 CelebA와 LSUN bedroom을 대상으로 한다.

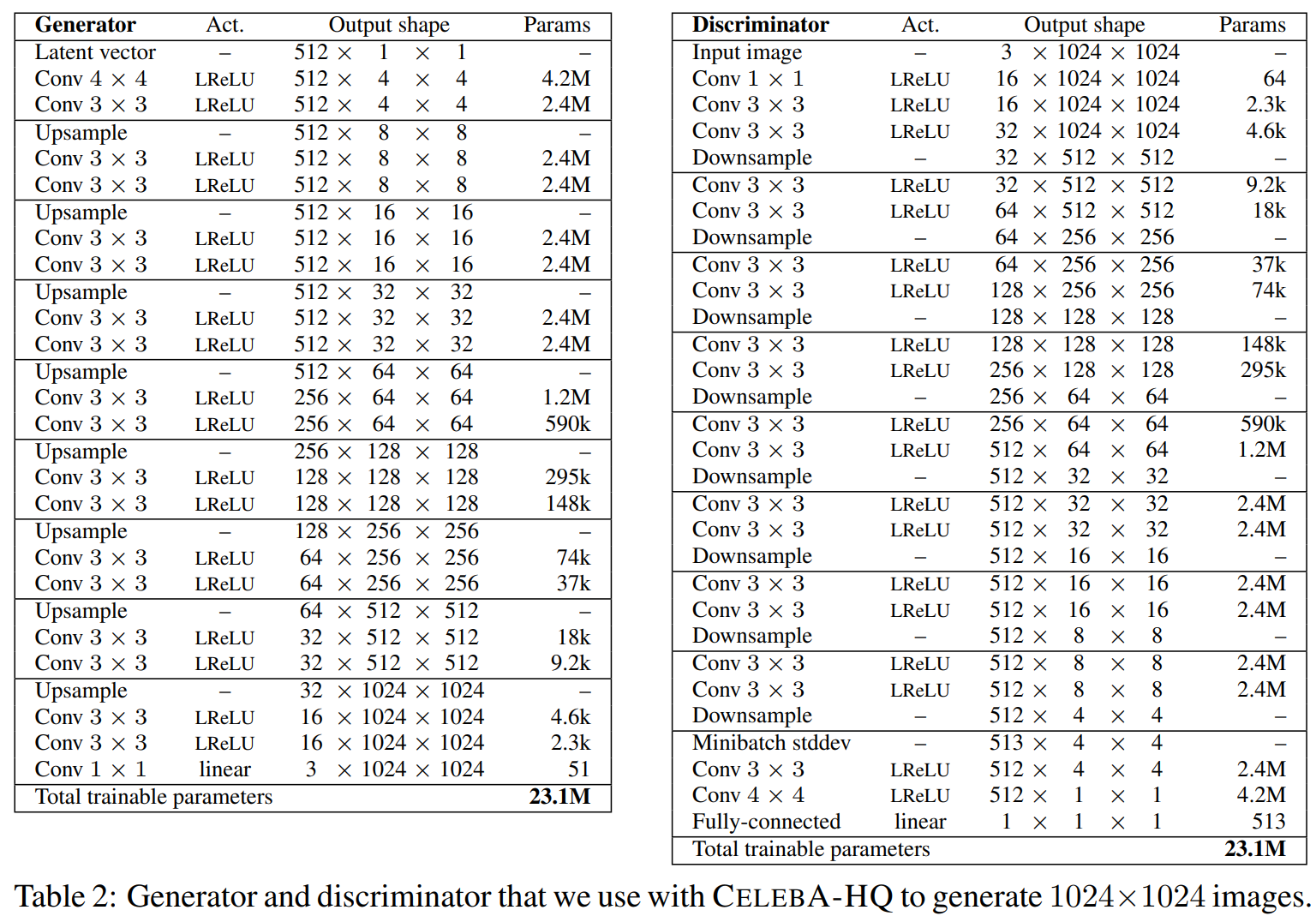
Untitled

https://www.youtube.com/watch?v=G06dEcZ-QTg

IMPORTANCE OF INDIVIDUAL CONTRIBUTIONS IN TERMS OF

STATISTICAL SIMILARITY

논문에서 제안한 모델의 구성요소의 평가와 평가지표의 유효함을 보이기 위해 SWD와 MS-SSIM을 평가 지표로 하여 실험을 진행한다. 비교 실험의 결과를 보이기 쉽게 하기 위해 discriminator가 천만 쌍의 실제 이미지를 보면 학습이 종료하였다. 또한 모델의 용량을 작게 잡았다.

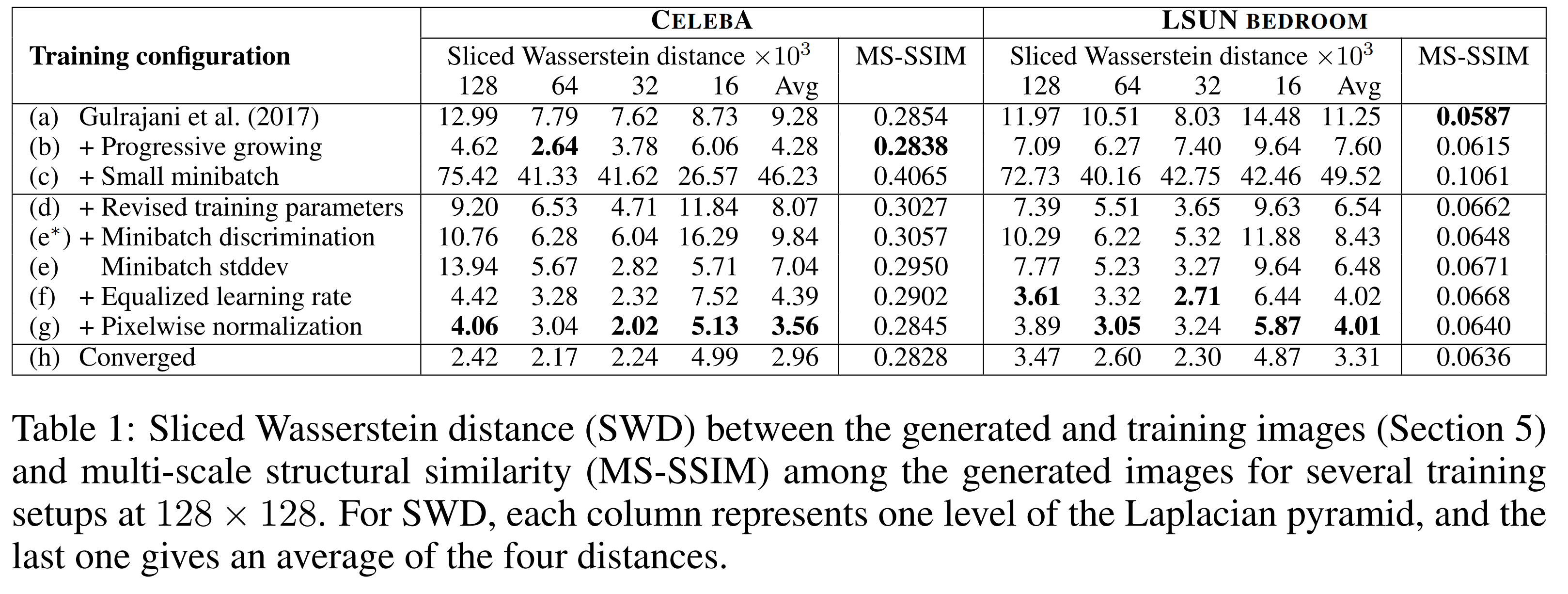
Untitled

(a)는 WGAN으로 baseline이다. (a)-(g)는 학습이 수렴되지 않은 것이며 (h)가 완전 수렴할 때까지 학습시킨 결과다.

(a)은 WGAN으로 generator에 batch normalization, discriminator에 layer normalization이 적용되어있다. 또한 batch size가 64다.

(b)는 Progressive Growing를 적용한 실험으로 SWD가 큰 폭으로 개선되었음을 볼 수 있다.

(c)는 batch size를 16으로 줄인 것으로 현실적으로 가능한 메모리를 감안한 것이다. 그 결과 SWD와 MS-SSIM 모두 큰 폭으로 증가하며 Figure3의 (c)를 보면 생성하는 이미지가 부자연스러워진 것을 확인 할 수 있다.

(d)에서는 hyperparameter를 바꾸고 generator에 batch normalization, discriminator와 layer normalization를 제거한 결과입니다.

(e*)는 기존(Salimans et al.,2016년) 의 minibatch discriminator 을 사용하는 실험이다. minibatch discriminator가 생성이미지의 다양성을 증가하도록 유도하는 것으로 알려진 만큼 MS-SSIM가 개선될 것 같았지만 MS-SSIM와 SWD를 모두 줄이지 못하였다.

(e)는 논문에서 제안한 단순화된 MiniBatch StdDev를 minibatch discriminator대신 사용하는 실험이다. (e*)와 달리 MS-SSIM을 개선하며 생성이미지 다양성 증가에 기여하는 것을 볼 수 있다.

나머지 (f) 및 (g) 실험은 equalized learning rate와 pixelwise normalization을 추가한 실험으로 SWD이 개선되고 생성된 이미지의 품질이 좋아진 것으로 보인다. (논문에서는 이야기가 없지만 (f)와 (g)에서 반영된 변경사항의 목적이 학습속도 개선과 안정화라는 점을 고려할 때 동일한 양의 학습데이터로 학습의 수렴이 조금 더 진행 되었기 때문이 아닐까 생각한다. )

평가지표 비교

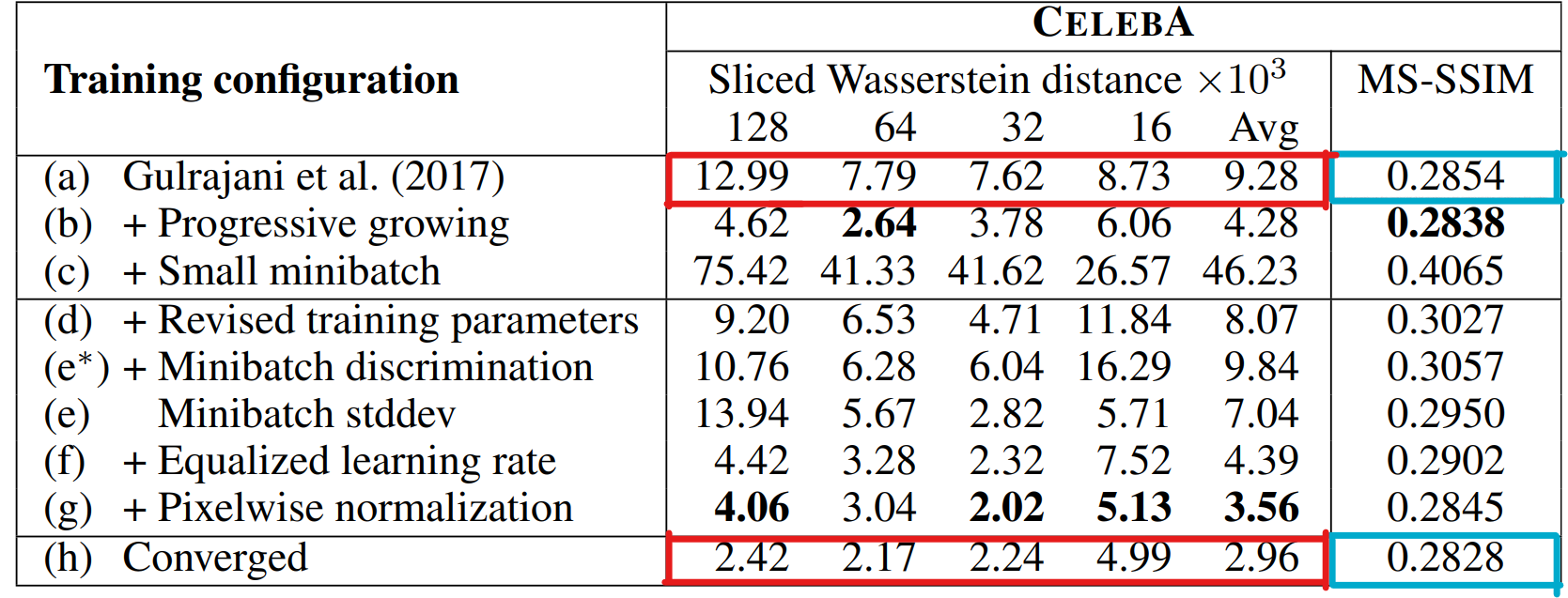
Figure3의 (a)와 (h)를 보면 (h)의 이미지가 훨씬 좋은 품질의 이미지인 것을 볼 수 있다. 하지만 Tabel 1에서 (a)열과 (h)열의 MS-SSIM 평가 지표를 보면 매우 비슷한 것을 볼 수 있다. 이것은 MS-SSIM이라는 지표는 생성 이미지의 다양성만을 평가하는 지표이고, 가짜 이미지와의 유사성을 평가하는 것은 아니기 때문이며. 한편, SWD의 수치는 생성이미지가 실제 이미지와 유사해지고 있음을 수치적으로 잘 반영하는 것을 볼 수 있다.

Untitled

Progressive Growing은 학습속도를 증가 시키는가?

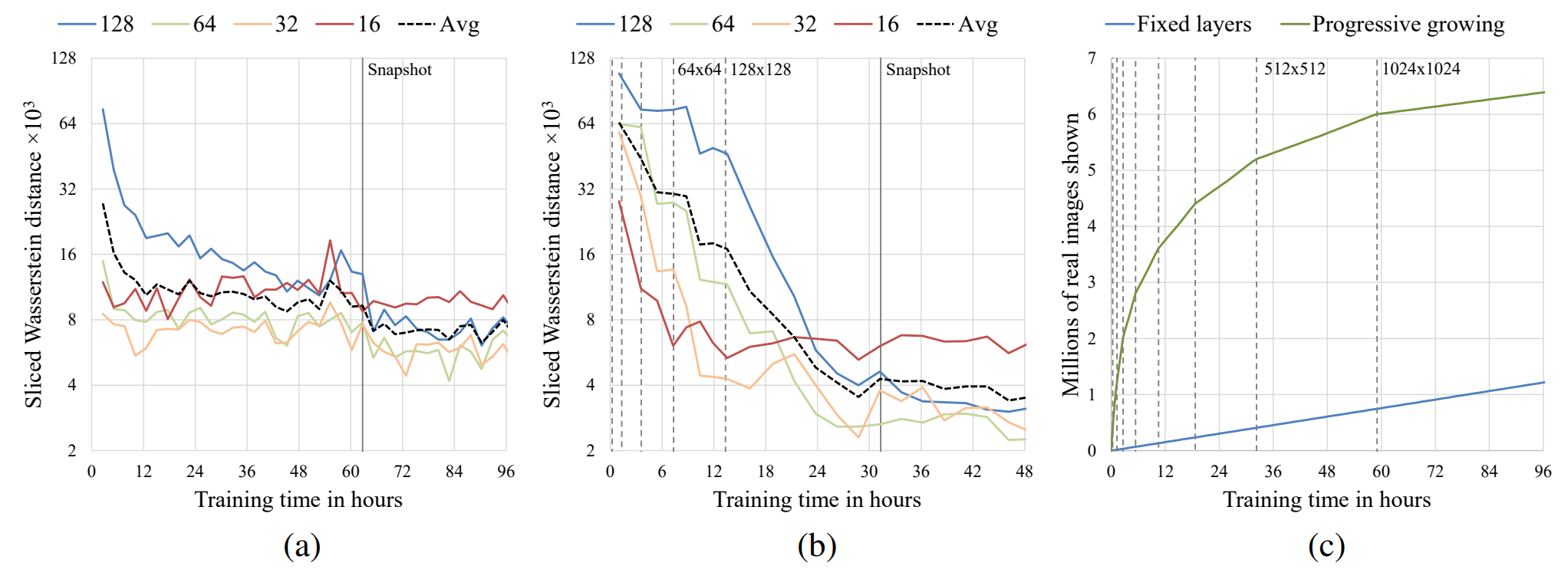
Untitled

Progressive Growing이 학습속도와 학습이 수렴하는데 기여하는 바를 보이기 위해 NVIDIA Tesla P100 환경에서 진행된 실험 결과다. 세로 점선은 해상도가 2배 증가하는 시간을 표시하고 (a),(b)의 그래프 색은 목표로 하는 생성이미지의 해상도를 의미한다.

(a)는 WGAN, (b)는 (a)와 동일한 네트워크에서 Progressive Growing만 적용하여 실험한 결과다. y축은 SWD를, x축은 학습시간이다.

(c)는 1024*1024 해상도의 이미지를 생성하도록 학습하는데 학습시간에 따른 Discriminator에 들어간 학습 이미지 수를 나타낸 그래프다.

학습속도 비교

(b)의 경우 (a)와 동일한 조건에서 Progressive Growing만을 적용하여 실험한 것이다. 약 2배 빠르게 학습이 수렴되며 수렴된 SWD도 Progressive Growing를 적용한 (b)가 우위에 있음을 보여준다.

Fixed layer로 학습할 때는 저해상도의 특징과 고해상도의 특징을 동시에 학습해야한다. 하지만, Progressive Growing를 적용하면 단계적으로 학습하게 되는데 (b)에서 보다시피 저해상도에서는 수렴속도가 빠르기 때문에 그 다음 층은 더 큰 해상도의 표현을 학습하는데 전념 할 수 있다.

(c): Progressive Growing를 적용하게 되면 학습 초기 저해상도를 학습할 때 모델의 크기가 작고 evaluate 속도가 빠르기 때문에 고정 시간내에 더 많은 이미지로 학습하게 된다. 학습이 진행되면서 해상도가 증가할수록 속도가 느려지며 1024*1024이미지를 학습할 때는 그래프의 기울기가 Fixed layer와 동일한 것을 볼 수 있다.

결과적으로 Progressive Growing를 적용하게 되면 5.4배의 학습 속도 향상을 기대할 수 있다.