IWAE
by Jongwon Park, Kyeongrok Park
IMPORTANCE WEIGHTED AUTOENCODERS(IWAE)
Yuri Burda, Roger Grosse, Ruslan Salakhutdinov [ICLR 2015]
본 포스팅은 IWAE(IMPORTANCE WEIGHTED AUTOENCODERS)논문을 정리한 문서입니다.
1. Preliminary: What is Latent Variable Model?
IWAE의 핵심 아이디어를 보기 전에 백드라운드로 latent variable model (LVM)에 대해 알아보겠다. 그림 1은 가장 심플한 LVM의 예시를 보여준다. 그림에서 x는 우리가 실제로 볼 수 있는 데이터 샘플이고, z는 우리가 볼 수 없지만 x를 생성하는데 사용되는 분포다.
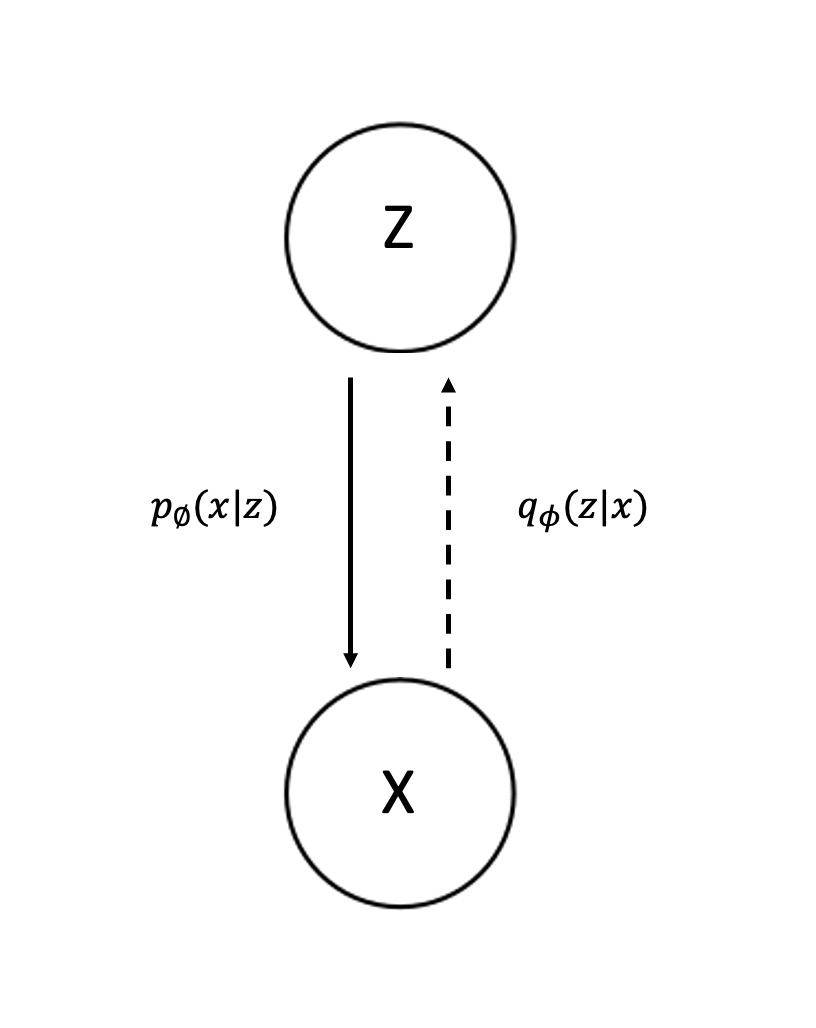
(그림 1 Latent Variable Model)
VAE에서는 z의 형태를 하나의 known distribution으로 정해 놓는 방식을 사용한다. 대표적으로 데이터가 discrete하면 bernoulli, continuous하면 gaussian 분포를 사용한다. 만일 z를 Bernoulli로 설정했다면, 아래와 같은 식을 통해 $p_{\theta}(x|z)$를 구할 수 있다. $$z = (z_{1},z_{2},...,z_{k}) \sim p(z;\beta) = \prod_{k=1}^{K} \beta_{k}^{z_{k}}(1-\beta_{k})^{1-z_{k}} $$ $$x = (x_{1},x_{2},...,x_{k}) \sim p(x|z) = Bernoulli(x_{i}; DNN(z))$$ z가 deep neural network와 sigmoid함수를 사용하여 0~1값을 준다면, x는 해당 값을 가지고 biased coin flipping을 하듯이 샘플링 할 수 있다. 샘플에 대한 likelihood evaluation은 다음과 같다. $$p_{\theta}(x) = \sum_{z} P_{z}(z)p_{\theta}(x|z)$$ 특정 x에 대해서, 모든 underlying cause(z)가 주어졌을 때 해당 x가 나올 확률들을 모두 더한다. $\sum$ 기호를 풀어보면 이해가 쉬울 것이다. z가 1부터 k까지의 값을 가질 수 있을 때, $p_{\theta}(x)$는 $p_{z}(z1)p_{\theta}(x|z1)+p_{z}(z2)p_{\theta}(x|z2)+...+p_{z}(zk)p_{\theta}(x|zk)$로 나타낼 수 있다. **Training은 N번 샘플된 x값들을 이용해서 likelihood evaluation을 maximize하는 $\theta$값을 찾는 과정이다.** Train objective는 다음과 같이 표현 할 수 있다. $$max_{\theta}\sum_{i}^{N}logp_{\theta}(x^{(i)}) = \sum_{i}^{N}log \sum_{z}^{K}p_{z}(z)p_{\theta}(x^{(i)}|z)$$ ### 이러한 과정은 K값이 작다면 아무런 문제가 되지 않는다. 만일 K값이 한정되어 있다면, 우리는 exact한 training objective를 얻을 수 있다. 예를 들어 $p_{\theta}(x|z)$가 mixture of 3 gaussians이고 $p_{z}(z)$가 uniform distribution이라고 해보겠다. $$p_{\theta}(x|z=k) = \frac{1}{(2\pi)^{\frac{n}{2}} |\sum_{k}|^\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{k})^{T}\sum_{k}^{-1}(x-\mu_{k}))$$ 이면서 $$p_{z}(z=A)=p_{z}(z=B)=p_{z}(z=C)$$이기 때문에 training objective는 다음과 같다. $$ \begin{align} \begin{split} max_{\theta}\sum_{i}logp_{\theta}(x^{(i)}) = \\ &+ max_{\mu, \sigma}\sum_{i}log[ \frac{1}{3}\frac{1}{(2\pi)^{\frac{n}{2}} |\sum_{A}|^\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{A})^{T}\Sigma_{A}^{-1}(x-\mu_{A})) \\ &+ \frac{1}{3}\frac{1}{(2\pi)^{\frac{n}{2}} |\sum_{B}|^\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{B})^{T}\Sigma_{B}^{-1}(x-\mu_{B})) \\ &+ \frac{1}{3}\frac{1}{(2\pi)^{\frac{n}{2}} |\sum_{C}|^\frac{1}{2}} exp(-\frac{1}{2}(x-\mu_{C})^{T}\Sigma_{C}^{-1}(x-\mu_{C}))] \end{split} \end{align} $$ 위 식의 모든 term은 계산이 가능하고 그 과정이 복잡하지 않다. 그림 2에서 볼 수 있듯이 Epoch이 지남에 따라 3개의 gaussian 분포로 나뉘는 것을 볼 수 있다.
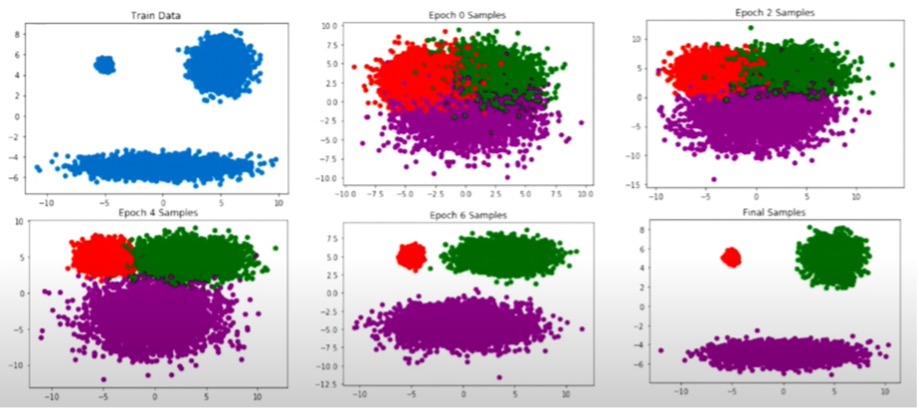
(그림 2 result) 4
## 2. Prior Sampling: Approximation for Large K 만일 training objective의 K값이 너무나도 커서 위의 예제처럼 전부 다 summation을 진행하는 게 불가능하다면 어떻게 해야 할까? 아래의 식 5처럼 z값을 샘플링 (prior sampling)해서 Monte Carlo방식으로 approximate하는 방법 밖에는 없을 것이다. 그 이후에는 동일하게 gradient descent 방식으로 $\theta$를 학습하면 된다. $$\sum_{i}^{N}log \sum_{z}^{K}p_{z}(z)p_{\theta}(x^{(i)}|z) \approx \sum_{i}^{N}log \frac{1}{K}\sum_{k=1}^{K}p_{\theta}(x^{(i)}|z_{k}^{(i)}) z_{k}^{(i)} ~ p_{z}(z)$$ 이것이 IWAE이전의 VAE모델들이 채택한 방식이다. 하지만 이와 같은 방식은 K값이 클수록 중요하지 않은 샘플들이 자주 추출되는 문제가 발생한다. ### 따라서 IWAE는 train objective에 $\frac{1}{K}\sum p_{\theta}(x^{(i)}|z_{k}^{(i)})$의 과정에서 중요하지 않은 샘플들이 뽑히는 문제를 다룬다 예를들어 그림 3과 같이 데이터가 여러 cluster들로 나뉘어 있고 $x^{(i)}$가 그중 빨간색 cluster 0에만 있다고 가정한다. Uniform distribution을 적용한다면 likelihood evaluation에서 $\frac{1}{5}$term만 유용할 것이다. 같은 논리로 K개의 cluster들로 나뉘어 있고, $x^{(i)}$가 마지막 cluster에 있다고 가정한다. 그러면 prior distribution z에서 uniform sampling을 진행했을 때 $\frac{1}{K}$ term만이 유용할 것이다.
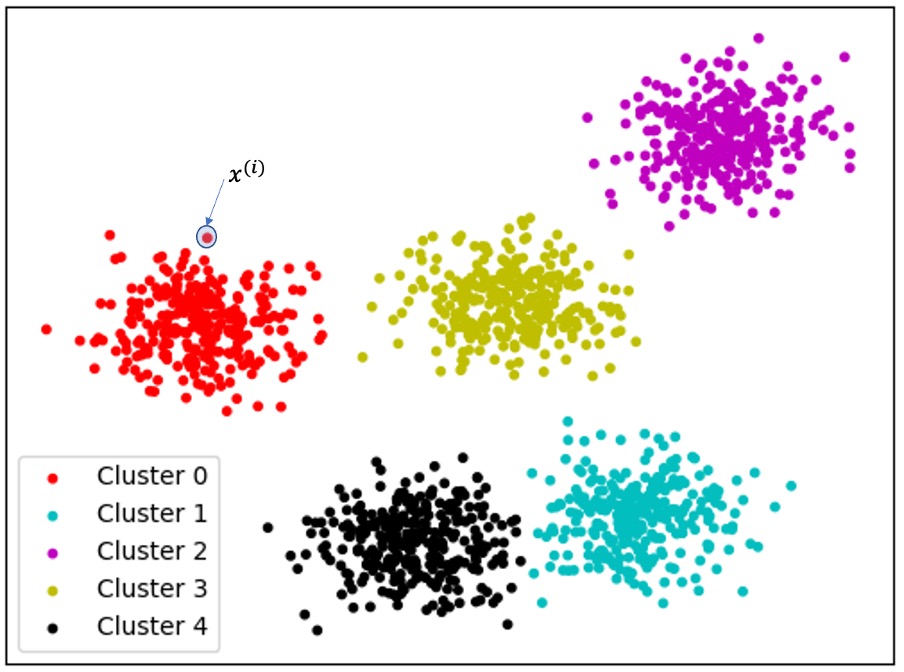
(그림 3 K-Clusters) 1
이해를 돕기 위해 likelihood evaluation을 뜻하는 3번식 $p_{\theta}(x) = \sum_{z} P_{z}(z)p_{\theta}(x|z)$을 다시 한 번 본다. 만일 우리가 MNIST데이터를 다루고 있고 (K=10), 숫자 1에 해당하는 데이터 $x^{(i)}$를 추출했다면, $p_{theta}(x) = \frac{1}{10}\times p_{\theta}(x^{(i)}|z_{1}) + \frac{1}{10}\times0 + ... + \frac{1}{10}\times0$가 될 것이다. $p_{\theta}(x^{(i)}|z_{2})$를 포함한 다른 cluster에서 숫자 1에 해당하는 데이터가 뽑힐 확률은 0이기 때문이다. **따라서 K값이 클수록 대부분의 샘플들은 meaningless해진다.** 수천번의 샘플링을 하고도 training에 도움이 전혀 안된다면 문제가 있다고 할 수 있다. ## 3. Importance Sampling: How to Sample Meaningful Data 우리의 목적을 다시 한 번 상기하자면, $E_{z \sim pz(z)}[p_{\theta}(x^{(i)}|z_{k}^{i})]$를 구하고 싶은 것이다. 그림 4를 통해 어떠한 경우에 문제가 되는 지 다시 한 번 보겠다.
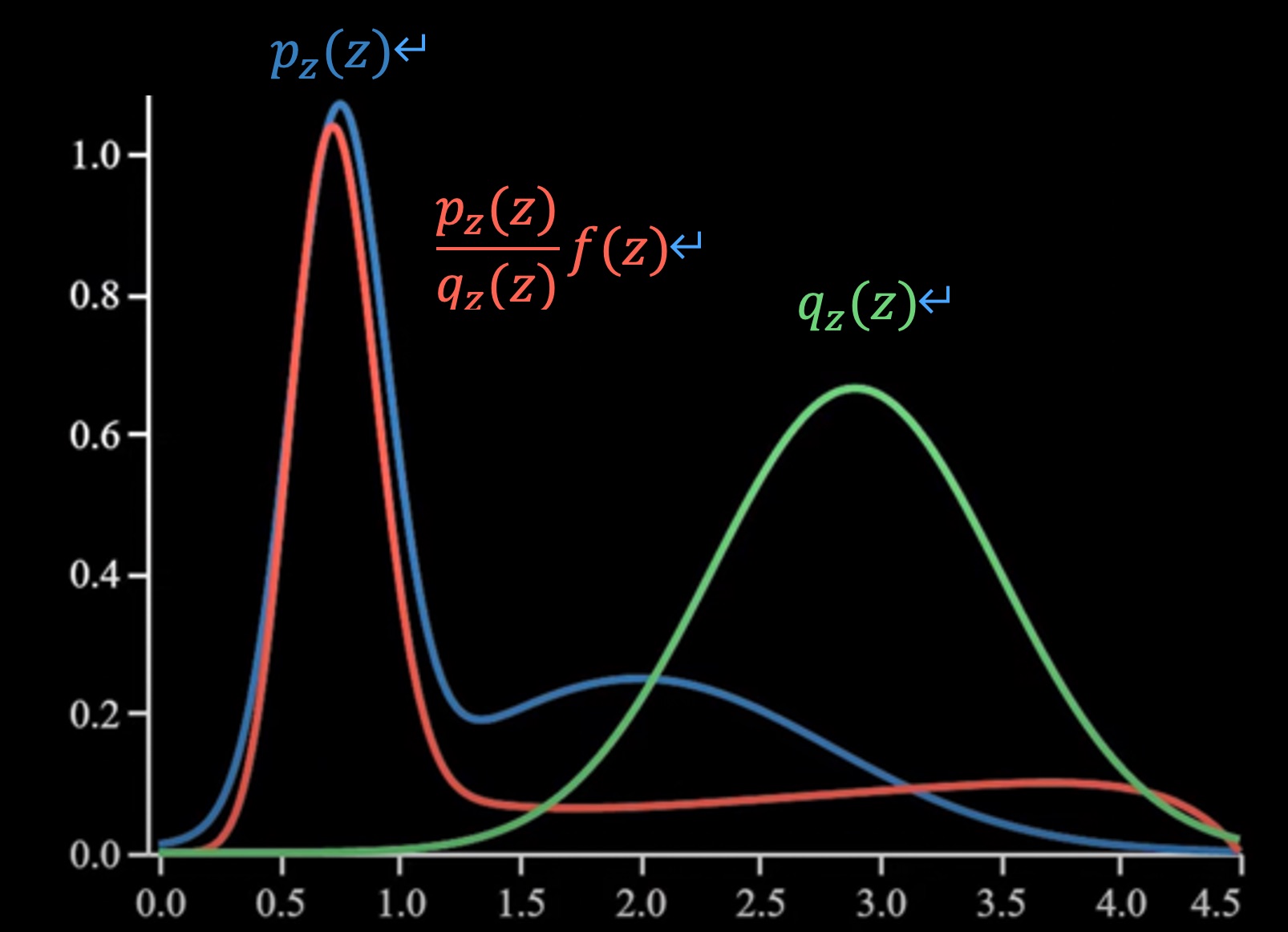
(그림 4 Problem Case) 3
그림 4에서 붉은색 $f(z)$가 $p_{\theta}(x^{(i)}|z_{k}^{i})$를 나타낸다. 그림에서 처럼 $p_{\theta}(x^{(i)}|z_{k}^{i})$가 높은 곳에서 $p_{z}(z)$가 낮으면 문제가 된다. $p_{z}(z)$에 따라 샘플된 데이터가 informative하지 않기 때문이다. $p_{\theta}(x^{(i)}|z_{k}^{i})$가 논문을 포함한 VAE모델에서 recognition network라고 지칭한다는 것을 알고 있다면, “VAE harshly penalizes approximate posterior samples which are unlikely to explain data, even if the recognition network puts much of its probability mass on good explanations.”라는 문장을 여기서 이해할 수 있다. VAE는 $p_{\theta}(x^{(i)}|z_{k}^{i})$값이 높더라도 $p_{z}(z)$값이 낮다면 해당 샘플을 사용하지 못한다. 앞서 보았듯이 likelihood evaluation이 0에 가까워지기 되기 때문이다. 이러한 경우에 Importance Sampling기법을 사용해서 $p_{\theta}(x^{(i)}|z_{k}^{i})$에 대해 informative한 q distribution을 새롭게 정의하고, q distribution을 따라 샘플링한 데이터로 $p_{z}(z)$에 대한 기댓값을 찾는다. Importance sampling의 수식 유도 과정은 다음과 같다. 편의를 위해 discrete한 데이터 분포를 가정하고, $p_{\theta}(x^{(i)}|z_{k}^{i})$를 $f(z)$로 놓는다. ### Importance Sampling Formulation $$ \begin{align} \begin{split} E_{z \sim pz(z)}[f(z)] \\ &= \sum_{z}p_{z}(z)f(z) \\ &= \sum_{z}\frac{q(z)}{q(z)}p_{z}(z)f(z) \\ &= \sum_{z \sim q(z)}\frac{p_{z}(z)}{q(z)}f(z) \\ &= E_{z \sim q(z)}[\frac{p_{z}(z)}{q(z)}f(z)] \\ &\approx \frac{1}{K}\sum_{i=1}^{K}\frac{p_{z}(z^{(i)})}{q(z^{(i)})}f(z^{(i)}) \quad with \quad z^{(i)} \sim q(z) \end{split} \end{align} $$ 위에서 볼 수 있듯이 이제는 $z^{i}$를 $q(z)$에서 샘플링하면서 원래의 train objective값을 구할 수 있다. 따라서 원래의 train objective가 $$\sum_{i}^{N}log \sum_{z}^{K}p_{z}(z)p_{\theta}(x^{(i)}|z)$$이었다면, 다음과 같이 변경된다. $$\approx \sum_{i}log\frac{1}{K}\sum_{k=1}^{K}\frac{p_{z}(z_{k}^{(i)})}{q(z_{k}^{(i)})}p_{\theta}(x^{(i)}|z_{k}^{(i)}) \quad with \quad z_{k}^{(i)} \sim q(z_{k}^{(i)})$$로 바뀌게 된다. 우리는 이러한 과정을 $f(z)$가 높은 곳에서 높은 값을 가지는 $q(z)$를 찾는 문제로 보았지만, 조금 다른 관점으로 $f(z) \times q(z)$가 높도록 $q(z)$를 설정하는 문제로도, $Var_{z \sim q}[\frac{p(z)}{q(z)}f(z)] < Var_{z~p}[f(z)]$가 되도록 하는 문제로도 볼 수 있다. 여기서 $\frac{p}{q}$로 $f(z)$를 reweight해주는 걸로 볼 수 있는데, 아래의 그림 5로 그럴 때 $p(z)$와 같아지는 것을 볼 수 있다. 다른 분포에서 뽑는 bias를 correct해주는 효과라고 이해할 수 있다. 또한 초록색 q확률을 따라 reweighted된 주황색 값을 뽑으면 그 variance가 매우 작음을 그림을 통해 확인 할 수 있다. 따라서 다른 sampling 방식들 (ex. rejection sampling)들과는 다르게 모든 샘플들을 사용할 수 있다.
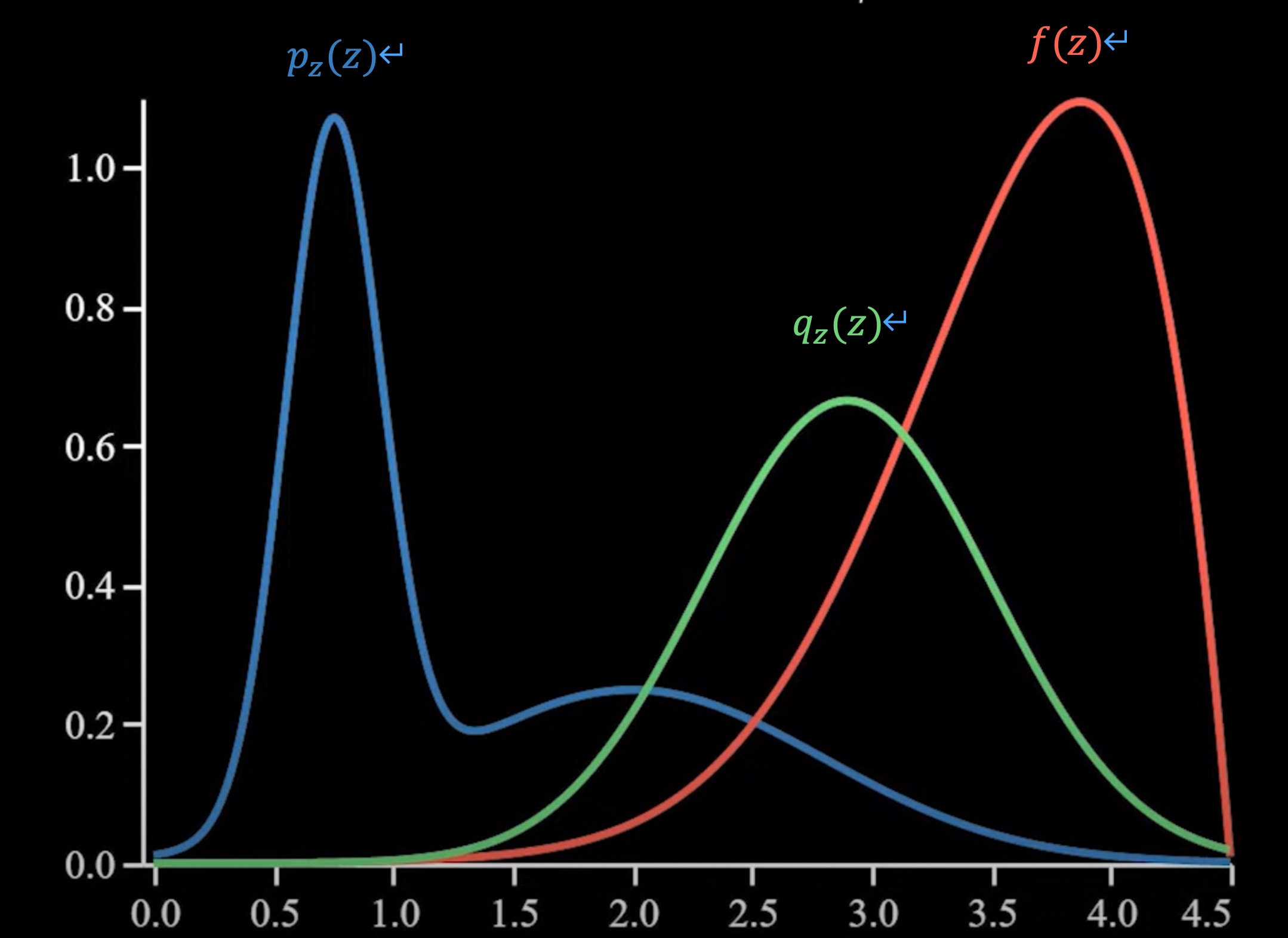
(그림 5 Solved Case) 3
## 4. Variational Approach for q(z): Ammortized Inference 이제 문제는 위에서 밝힌 조건들을 만족하는 좋은 q(z)를 찾는 것으로 바뀐다. 결국 샘플 $x^{(i)}$가 주어졌을 때 어떤 z가 informative한지 z를 uniform이 아닌 z sampler 를 통해 선정하는 것으로 볼 수 있다. 물론 Bayes rule을 사용하면 $p_{\theta}(z|x^{(i)}) = \frac{p_{\theta}(x^{(i)}|z) p_{z}(z)}{p_{\theta}(x^{(i)})}$가 되지만, 분모의 normalizing constant를 얻을 수 없기 때문에 $q(z)$를 샘플링하기 쉬운 known distribution으로 설정하는 variational approach를 사용한다. 논문에서는 Gaussian으로 설정하였고, KL divergence를 사용하여 근사시켰다. 전개하면 다음과 같다. $$ \begin{align} \begin{split} min_{q(z)}KL(q(z)||p_{\theta}(z|x^{(i)})) \\ &= min_{q(z)}E_{z \sim q(z)}log(\frac{q(z)}{p_{\theta}(z|x^{(i)})}) \\ &= min_{q(z)}E_{z \sim q(z)}log(\frac{q(z)}{p_{\theta}(x^{(i)}|z)p_{z}(z)/p_{\theta}(x^{(i)})}) \\ &= min_{q(z)}E_{z \sim q(z)}[logq(z)-logp_{z}(z)-logp_{\theta}(x^{(i)}|z)] + logp_{\theta}(x^{(i)}) \end{split} \end{align} $$ 이와같은 새로운 objective를 얻을 수 있다. 각 term을 모두 계산하는 것은 가능하지만 각 데이터 $x^{(i)}$마다 q를 찾는 건 비효율 적이기 때문에 같은 inference problem을 줄이기 위한 방법으로 Ammortized Inference방식을 사용해 효율적인 계산을 사용한다. 즉, q분포를 $\phi$ 파라미터를 가지는 Neural Network로 표현하는 것이다. 결국 다음과 같은 $min_{\phi}\sum_{i}KL(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))$식으로 q를 찾아낸다. 논문에서 “The recognition network generates multiple approximate posterior samples, and their weights are averaged.”는 이와 같은 f(z)에 informative한 amortized inferenced된 q분포에서 샘플을 얻는 부분을 의미한다. 이제 q(z)는 reparameterization trick을 사용한 gaussian 분포로 $$q_{\phi} = N(\mu_{\phi}(x), \sigma_{\phi}^{2}(x)), \quad Equivalently: z = \mu_{\phi}(x)+\epsilon\sigma_{\phi}(x), \quad \epsilon \sim N(0,I)$$로 표현 될 수 있고, 그림 1의 Latent variable Model에 점선으로 표현된 inference 과정을 의미한다. ## 5. Final Objective Function of IWAE 결론적으로 IWAE의 objective function은 latent variable model의 objective인 $$max_{\theta}\sum_{i}^{N}logp_{\theta}(x^{(i)}) = \sum_{i}^{N}log \sum_{z}^{K}p_{z}(z)p_{\theta}(x^{(i)}|z)$$에서 Importance Sampling을 통해 $$\approx \sum_{i}log\frac{1}{K}\sum_{k=1}^{K}\frac{p_{z}(z_{k}^{(i)})}{q(z_{k}^{(i)})}p_{\theta}(x^{(i)}|z_{k}^{(i)}) \quad with \quad z_{k}^{(i)} \sim q(z_{k}^{(i)})$$ 다음과 같이 변형된 것과, ammortized inference를 사용해 q분포를 제한다면서 $$min_{\phi}\sum_{i}KL(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)}))$$을 동시에 사용하게 된다. 따라서 final objective function은 $$max_{\theta,\phi}(\sum_{i}log\frac{1}{K}\sum_{k=1}^{K}\frac{p_{z}(z_{k}^{(i)})}{q(z_{k}^{(i)})}p_{\theta}(x^{(i)}|z_{k}^{(i)}) - \sum_{i}KL(q_{\phi}(z|x^{(i)})||p_{\theta}(z|x^{(i)})))$$이 된다. ## 6. Variational Auto-Encoder(VAE)와의 비교 IWAE는 기존의 VAE방식의 발전된 방법론으로 알려져 있다. 둘의 직접적인 비교를 위해 VAE를 짧게 소개한다. 추가적인 설명은 이번 포스팅 이전에 있는 VAE와 SBAI(Stochastic Backpropagation and Approximate Inference in DGM) 포스팅을 통해 학습할 것을 추천한다. VAE는 generation process $p(x|\theta)$와 recognition model $q(h|x)$를 여러 non-linear hidden layer(h)를 통한 ancestral sampling으로 학습한다. 각각 $$p(x|\theta) = \sum_{h^1,...,h^L}p(h^L|\theta)p(h^{L-1}|h^L,\theta)...p(x|h^1,\theta)$$ $$q(h|x) = q(h^1|x)q(h2|h1)...q(h^L|h^{L-1})$$ 로 나타낸다. 여기서 prior distribution과 conditional distributions $p(h^l|h^{l+1})$과 $q(h^l|h^{l-1})$은 모두 Normal Gaussian을 정의한다. 이 정의에 따라 기존 VAE의 objective function은 ELBO라고 불리는 $$logp(x) \geq E_{q(h|x)}[log\frac{p(x,h)}{q(h|x)}]$$이다. 이때 IWAE와 똑같이 q를 parameterize해준다면 VAE의 gradient식은 아래와 같다. $$\nabla_{\theta}logE_{h \sim q(h|x,\theta)}[\frac{p(x,h|\theta)}{q(h|x.\theta)}] = E_{\epsilon^1,...,\epsilon^L} \sim N(o,I)[\nabla_{\theta}log \frac{p(x,h(\epsilon,x,\theta)|\theta)}{q(h(\epsilon,x,\theta)|x,\theta)}]$$ 이에 반해 IWAE의 gradient는 다음과 같다. $$E_{\epsilon \sim N(0,I)}[\frac{1}{k}\sum_{i}^{K}\nabla_{\theta}log \frac{p(x,h(\epsilon_{i},x,\theta)|\theta)}{q(h(\epsilon_{i},x,\theta)|x,\theta)}] = \sum_{i=1}^{k}\tilde{w_i}\nabla_{\theta}logw(x,h(\epsilon_i,x,\theta),theta)$$ with importance weight $$w(x,h,\theta) = \frac{p(x,h|\theta)}{q(h|x,\theta)}$$ and normalized importance weight $$\tilde{w_i}= w_i/\sum_{i=1}^{k}w_i$$ **VAE의 gradient식과 IWAE의 gradient식은 k=1로 두면 완전히 동일함을 볼 수 있다.** ### Tighter Lower Bound & More spead-out over predictins IWAE와 standard VAE의 objective에 두 가지 차이가 있음을 저자는 논문에서 밝히고 있다. 첫 번째로 IWAE의 objective는 다음과 같이 두개의 term으로 분해 될 수 있다. $$\nabla_{\theta}log w(x,h(\epsilon_i,x,\theta),theta) = \nabla_{\theta}log p(x,h(x,\epsilon_i,\theta)|\theta) - \nabla_{\theta}log q(h(x,\epsilon_i,\theta)|x,\theta)$$ 첫 term은 recognition network가 hidden representation에 adjust 함으로써 더 좋은 예측을 만들어 내는 것, 두 번째 term은 recognition network가 predictions들에 대해 더 spread-out distribution을 가지도록 하는 것이다. 이러한 objective를 통한 update는 importance weight로 곱해진 샘플들의 평균으로 일어난다. spead-out distribution에 대한 설명은 논문에 나와있지 않지만 "Tackling Over-pruning in Variational Autoencoders"논문에 따르면 VAE의 over-pruning 문제를 해결한 중요한 property이다. 이는 Experiment때 다시 한번 돌아오겠다. 두 번째로 저자는 IWAE가 더 tigher한 lower bound를 가지고 있음을 증명하고 있다. $$log p(x) \geq L_{k+1} \geq L_{K}$$에 대한 증명은 다음과 같다. $$L_k = E_{h}[log\frac{1}{k}\sum_{i=1}^k\frac{p(x,h_i)}{q(h_i|x)}] \geq E_{h}[E_{I={i_1,...,i_m}}[log\frac{1}{m}\sum_{j=1}^m \frac{p(x,h_{ij})}{q(h_{ij}|x)}]] = L_m$$ 해당 증명은 논문의 appendix에 더 상세히 적혀있음으로 본 논문을 참고하는 것을 추천한다. ## 7. Experiment 논문에서 제공한 실험 결과 테이블은 두 가지이다.
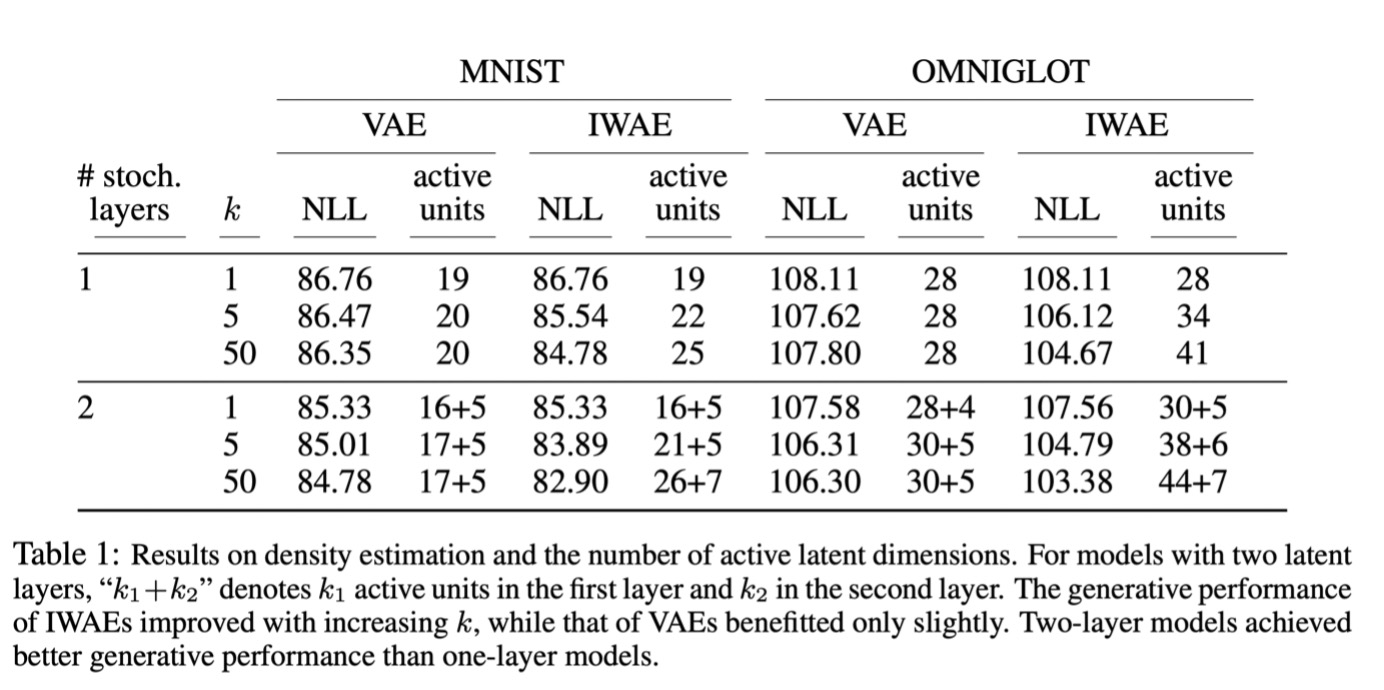
(그림 6 Table 1)
테이블 1은 IWAE와 VAE의 전반적인 결과를 보여준다. IWAE가 VAE보다 전반적으로 더 좋은 결과를 보여주며, K 수를 늘릴 때 IWAE는 확실히 NLL이 낮아지는 것을 볼 수 있다. 두 모델 전부 레이어 수를 2로 늘릴 때 더 좋은 결과를 보여준다.
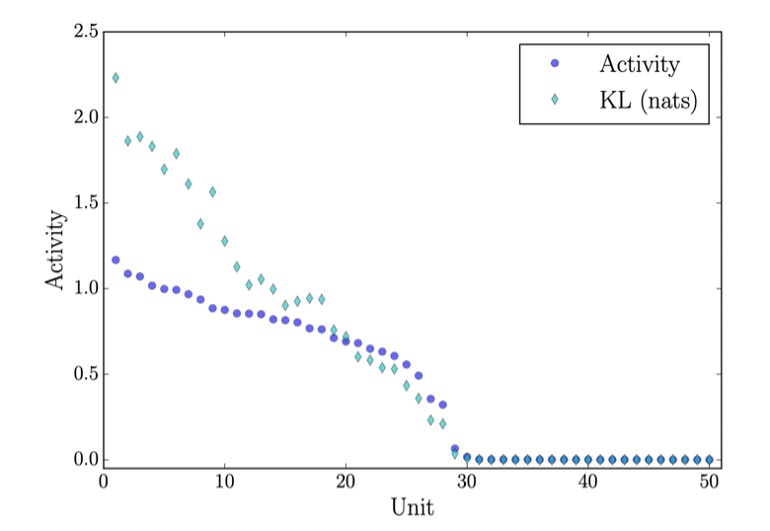
(그림 7 Correlation between active units and KL) 5
Inactive units은 collapsed to the prior문제를 나타낸다. 다른 표현으로는 over-pruning problem이라고 부른다. 모든 데이터를 표현하기 위해서는 D-dimension이 필요할지라도, each individual example은 훨씬 작은 d-dimension으로도 표현 할 수 있다. D-dimension과 더 작은 d-dimension간의 차이만큼 inactive units가 발생한다고 볼 수 있다. IWAE는 위에서 보았듯이 prediction distribution을 더 spead-out하게 하는 objective function을 가지고 있어 generalize power가 강하기 때문에 active units이 더 많다고 볼 수 있다.
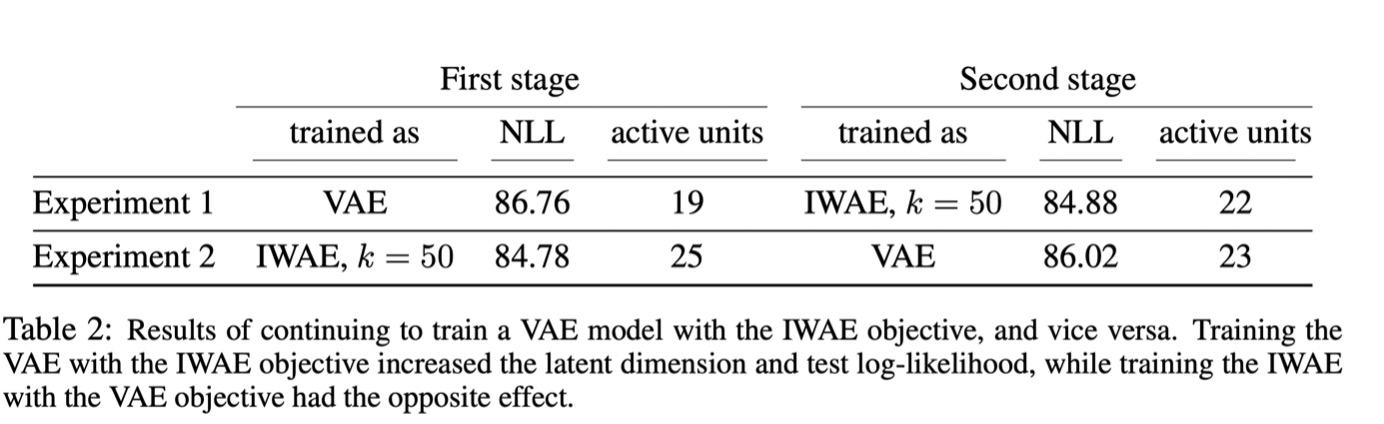
(그림 8 테이블 2)
테이블 2의 experiment1은 VAE objective로 training을 시작한 후 IWAE objective로 변경한 것이고, experiment 2는 IWAE objective로 시작한 후 VAE objective로 변경한 것이다. 실험 결과가 saddle point나 local minimizer같은 문제로 대변되는 optimization 문제가 아닌 objective functions 으로 인해 나온 의도된 결과임을 보여주는 실험이다. ## 8. Potential Short-Coming & Future Work IWAE는 의심의 여지없이 VAE의 발전된 방식이지만, 많은 문제점을 내포하고 있다. 가장 큰 문제점은 q분포를 정하는 방식과 sampling방식 자체의 한계일 것이다. q분포를 정하는 데 있어 편의를 위해 Gaussian혹은 Bernoulli분포를 사용하지만, 실제 분포와 그 차이가 클 수 있다. 분포의 형태도 다르지만 특히 Ammortized inference방식에서 오는 오차도 무시할 수 없다. 여기서는 해당 문제들을 해결하려고 노력한 두 가지 논문을 짧게 소개한다. ### Nowozin, Sebastian. "Debiasing evidence approximations: On importance-weighted autoencoders and jackknife variational inference." International conference on learning representations. 2018. 해당 논문은 IWAE의 bound를 biased estimator라고 정의하고, 그 bias를 줄이는 데 Jacknife bias correction방식을 사용한다. 기존 논문의 가장 큰 한계점을 뽑으라면 importance sampling에서 발생하는 variance가 작다는 것을 mean absolute deviation (MAD)을 통해 low variance를 간접적으로만 증명한 것이라고 생각한다.
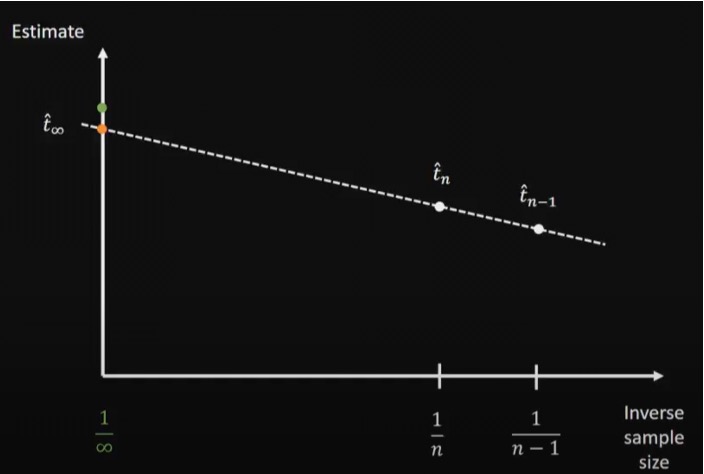
(그림 9 Jacknife bias correction) 2
Jacknife방식은 1954년 처음 소개된 방식으로 그 동작 방법이 매우 간단하다. 기존의 샘플링 방식은 n개의 샘플로 $\hat{t}$을 예측한다. 하지만, 다양한 갯수의 샘플로 예측한 값을 함께 사용하면 bias를 줄일 수 있다. 그림 9에서 볼 수 있듯이 n개만 사용하면 $t_{green point} - \hat{t}\_{n}$의 bias가 존재하지만, $\hat{t}\_{n-1}$의 값을 함꼐 사용하여 linear approximation을 진행하면 $t\_{green point} - \hat{t}\_{\inf}$의 훨씬 작은 bias만이 존재하게 된다. 해당 논문은 이러한 방식을 통해 실제 bias값을 줄인 것 이외에도 이론적으로 IWAE의 bias와 variance를 연구한 것이 주요 contribution이다. ### Yin, Mingzhang, and Mingyuan Zhou. "Semi-implicit variational inference." International Conference on Machine Learning. PMLR, 2018. 두 번째 소개할 논문은 semi-implicit variational inference(SIVI)방식을 제시한 논문이다. (semi)implicit distribution이란 샘플을 추출할 수는 있지만 closed-form density가 없는 distribution을 의미한다. q가 parametize가 될 때 $q_{\phi}(z|\psi)$가 analytically tractable하고 $q_{\phi}(z|\psi)$와 $q_{\phi}(\psi)$가 reparameterize 가능하다면 다음 식과 같이 semi-implicit한 $q_{\phi}(z)$를 찾을 수 있다. $$q_{\phi}(z) = \int q_{\phi}(z|\psi)q_{\phi}(\psi)d\psi $$ 훨씬 더 flexible한 q분포를 사용할 수 있으므로 더 정확한 variational inference가 가능해진다.
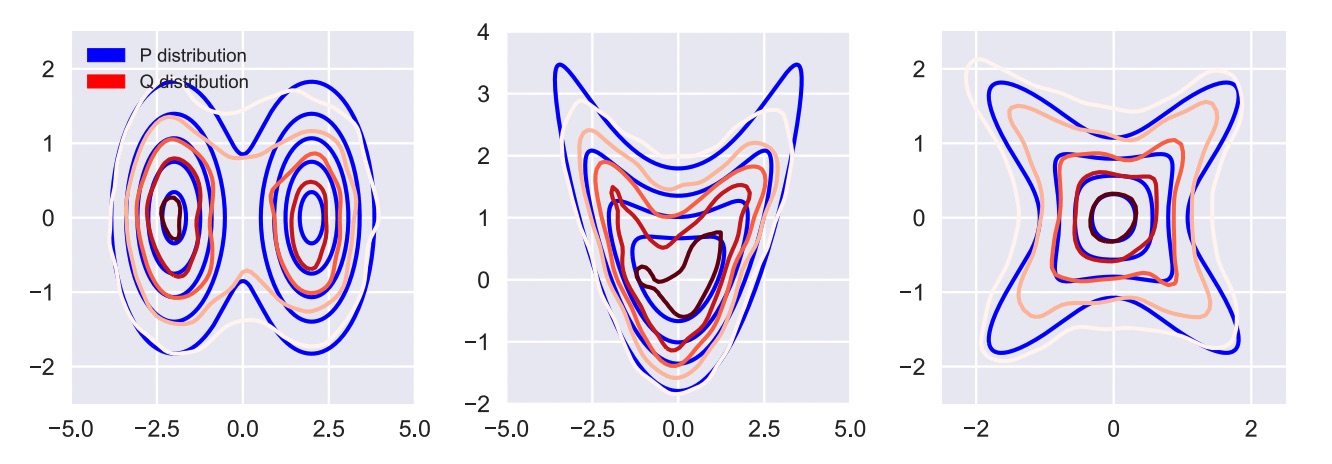
(그림 10 Approximating target distribution with SIVI) 5
그림 10을 보면 q분포가 기존의 Gaussian모양을 벗어나서 multi-modal한 모습과 매우 flexible한 모습을 보여주는 것을 볼 수 있다. 해당 방식은 VAE라는 큰 필드에서의 발전으로 graph neural network를 포함한 매우 다양한 분야에서 사용이 되고 있다. --- **Reference** [1] IKKIson. “8. 빅데이터 처리 과정 기술 (3) 분석.” 이끼의 생각, TISTORY, 23 May 2019, https://
Subscribe via RSS
