Markov Chain Monte Carlo and Variational Inference: Bridging the Gap.
by Sungmin Kang
- Tim Salimans, Diederik P. Kingma, and Max Welling. Markov Chain Monte Carlo and Variational Inference: Bridging the Gap. Proceedings of the 32nd International Conference on Machine Learning, 2015
Introduction
Markov Chain Monte Carlo(MCMC)는 보다 정확한 모델을 계산할 수 있지만 샘플링에 시간이 매우 오래 걸리는 단점이 있고, Variational Inference(VI)는 드는 시간을 단축시켰지만 모델의 표현력이 떨어지는 문제가 존재합니다. 본 논문 Markov Chain Monte Carlo and Variational Inference: Bridging the Gap(이하 MCMC and VI)에서는 두 개의 간극을 메우는 방법을 제시하고, 이 방법의 실제 구현으로 Hamiltonian VI 구현체를 제시합니다.
Markov Chain Monte Carlo
Variational Inference는 강의 내용에서도, 다른 논문의 포스팅에서도 많이 다루어졌으므로 내용은 생략하고, Markov Chain Monte Carlo에 대해 간략하게 설명하고 넘어가도록 하겠습니다.
Monte Carlo
무작위로 매우 많은 시행을 할 경우, 실제 값에 근사한 결과가 나오는 것을 활용합니다. 이 예시로 흔히 보신 것은 -1~1 사이에 점을 무수히 많이 찍어서, 원 범위 안에 있는 점의 개수를 구한 뒤, 원주율을 근사하는 것이 있을 것 같습니다. 실제로 적절한 무작위 생성이 있다면 시행 횟수가 늘어남에 따라 실제 원주율 값에 근사하는 것을 보실 수 있습니다.
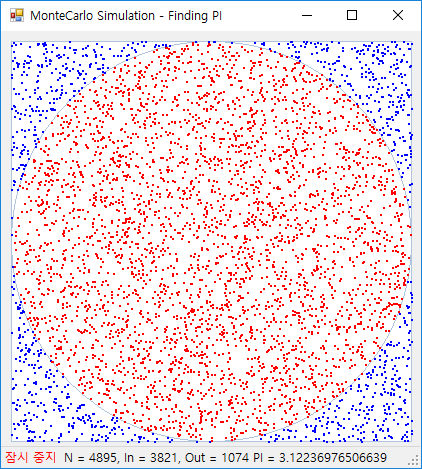
Monte Carlo 방법으로 원주율 추측, 출처: 네이버 블로그
Markov Chain
Markov Chain은 이전의 상태만을 바탕으로 현재의 상태에 영향이 가도록 구성된 체인입니다. 간단한 예시를 들자면, 어제 비가 왔을 때 오늘 비가 올 확률과 오지 않을 확률이 있고 - 어제 비가 오지 않았을 때 오늘 비가 올 확률과 오지 않을 확률이 제시된 상황을 생각해보시면 됩니다.
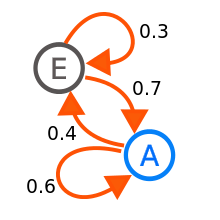
Monte Carlo 방법으로 원주율 추측, 출처: wikipedia
Monte Carlo + Markov Chain
둘을 결합한 Markov Chain Monte Carlo는, Markov Chain에서의 확률을 바탕으로 실제로 무작위 샘플링을 통해 시뮬레이션하는 Monte Carlo식으로 하는 것입니다. 즉, 이전 상태값을 활용한 무작위 동작을 무한히 반복한다면, 실제 분포와 근사한 분포를 얻을 수 있다는 것입니다.
‘이 이전 상태값을 활용한 무작위 동작’은 여러가지 방식이 있습니다. 간단한 예시인 Metropolis 알고리즘을 예로 들면, 현재 위치에서 정규분포상의 무작위 값을 바탕으로 근처로 이동을 시도합니다. 이동했을 때의 가능성이 더 높다면 실제로 이동하고, 그렇지 않다면 거절합니다. 다만 때때로 거절할 상황에도 수용하는 상황이 생깁니다.
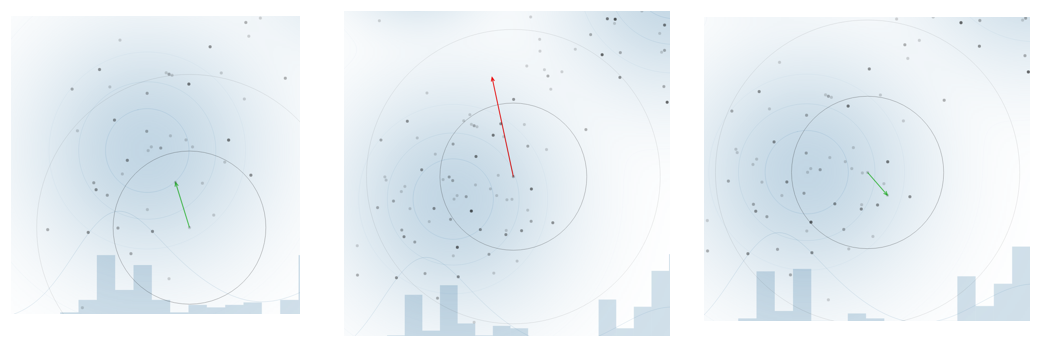
왼쪽은 더 가능성이 높아 이동한 경우, 중앙은 가능성이 더 낮아져 이동하지 않은 경우, 오른쪽은 가능성이 낮아지는 경우임에도 수용한 경우입니다. 이러한 동작을 반복하면 실제 분포를 얻어낼 수 있게 됩니다.
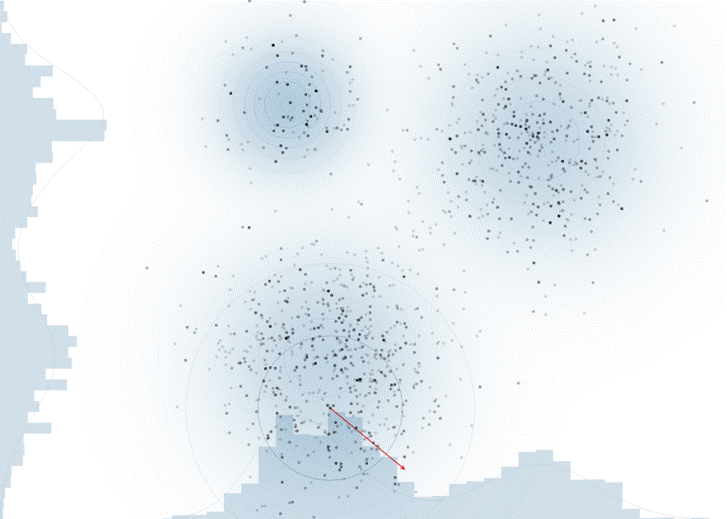
위 시뮬레이션은 https://chi-feng.github.io/mcmc-demo/app.html 에서 직접 수행해보실 수 있습니다.
This paper
Background
위에서 설명드린 내용을 바탕으로, MCMC는 점근적으로(asymptotically) 정확해집니다. 다만 이 과정에서 극도로 많은 시뮬레이션이 필요할 것이므로 느립니다. 더불어 좋은 Markov Chain을 구성하는 데에 어려움이 있고, 값이 실제에 근사했는지를 확인하는 것조차 어렵습니다.
이에 반해 VI는 정확한 분포를 예측할 수 있다는 사실 자체를 보장할 수 없는 문제가 있지만 더 빠르게 수행할 수 있습니다.
Contribution
본 논문은 MCMC가 실제 분포에 근사할 수 있다는 가능성과, VI의 낮은 비용을 가져오는 것을 제안합니다. 더불어 이의 실제 구현체인 Hamiltonian VI를 Auxiliary variable과 Stochastic Gradent VI를 활용하여 만들었습니다.
MCMC, more details
앞서 설명드렸던 Metropolis의 일부분에서, 단순히 정규분포 값을 활용해서 이동한다면 Local Optima에 갇히는 현상이 발생하게 됩니다. 이를 해결하기 위해 일정 수준 이하로 가능성이 낮아지는 경우 수용하도록 한 것이 Metropolis 알고리즘입니다. 다만 이러한 경우에도 Local Optima 근처에서 맴도는 현상이 종종 발생하는 단점은 존재합니다.
이러한 MCMC의 단점을 해결하는 것은 더 좋은 Markov Chain을 구성하는 것, 즉 더 나은 샘플링 기법을 고안하는 것입니다. 이를 위해서는 본 논문에 제시된 Gibbs Sampling, Over-relaxation 등을 포함하여 Hamiltonian MC(HMC) 등의 많은 기법이 연구되고 있으며 Jiaming Song (2017) A-NICE-MC: Adversarial Training for MCMC 과 같은 관련 논문도 제시되고 있습니다.
MCMC and Auxiliary Variables
논문 내용의 시작은 VI에서 시작합니다. VI에서 얻어온 아래 식 (1)과 (2) 두 개를 바탕으로 시작합니다.
\[\begin{align} \log {p(x)} &\geq \log{p(x)} - D_{KL}(q_\theta(z|x)||p(z|x)) \\ &= \Bbb{E}_{q_\theta(z|x)}[\log{p(x,z)}-\log{q_\theta(z|x)}]=\mathcal{L}. \end{align}\]이제 여기에 $y=z_0, z_1, …, z_{t-1}$ 인 auxiliary random variable $y$를 도입합니다. 그렇다면 $q(z|x)=q(z_0|x)\prod_{t=1}^{T}q(z_t|z_{t-1},x)$임을 볼 수 있습니다.
위 식을 식 (2)에 대입한다면,
\[\begin{align} \mathcal{L}_{\text{aux}} \\ &= \Bbb{E}_{q(y, z_T|x)}[\log[p(x,z_T)r(y|x,z_T)]-\log{q(y,z_T|x)}] \nonumber \\ &= \mathcal{L} - \Bbb{E}_{q(z_T|x)}\{D_{KL}[q(y|z_T,x)||r(y|z_T,x))]\} \nonumber \\ &\leq \mathcal{L} \leq \log[p(x)] \nonumber \end{align}\]식을 얻을 수 있습니다. 이 때 $r(y|x,z_T)$가 임의로 정한 auxiliary inference distribution이며, markov chain을 따르도록 구성했으므로 $q_\theta(z|x)$가 $q(y,z_T|x)$가 됩니다. 이 식에서는 markov chain을 거쳐서 연쇄적으로 $z$를 $z_0$에서 $z_{t-1}$로 가는 과정을 auxiliary variable의 도입으로 보충해준 식이라 보시면 됩니다. 즉, 이 과정 전체에 대해서 $z$ 자리에 $z_T$값을 바로 넣을 수 없기 때문에 보조 변수를 도입해서 그 사이의 상관관계를 설명할 수 있는 새로운 분포를 넣어준 것입니다.
이 상황에서 $r$이 $q$를 그대로 묘사하는 것이 최적인 상황일 것입니다. 그러나 $q$가 intractable할 가능성이 있으므로 $r~q$가 되도록, 그러면서도 최대한 expressive하게끔 $r$을 자유롭게 택합니다. 그러면 $q$가 markov rule을 따르는 상황이므로, $r$ 역시도 markov rule을 따르는 것으로 만들면 적절할 것입니다.
위 내용을 바탕으로 variational lower bound를 구하게 되면
\[\begin{align} \log{p(x)} &\geq \Bbb{E}_q[\log{p(x,z_T)}-\log{q(z_0,...,z_T|x)} \\ &+\log{r(z_0,...,z_{t-1}|x, z_T)]} \nonumber \\ &= \Bbb{E}_{q}[\log[p(x,z_T)/q(z_0|x)] \nonumber \\ &+ \sum_{t=1}^{T}\log[r_t(z_{t-1}|x,z_t)/q_t(z_t|x,z_{t-1})] \nonumber \end{align}\]를 얻을 수 있습니다.
앞서 설명드렸듯 $r$이 markov rule를 따르는 상황에서 정리한 식 (4)에서, $\sum_{t=1}^{T}\log[r_t(z_{t-1}|x,z_t)/ q_t(z_t|x,z_{t-1})]$ 부분을 확인하면 $r_t$가 $q_t$의 inverse model임을 볼 수 있습니다.
이 식 (4)를 활용하면 논문에 제시된 Algorithm 1인 MCMC 단계별 하한값을 구할 수 있게 됩니다.

논문 내 Algorithm 1
이 알고리즘은 unbised, 즉 모델의 평균과 실제의 차이인 bias가 0인, 평균 자체는 정확한 값을 얻어낸다고 합니다. 따라서 평균은 같은 점을 활용해서 여기에 $z_t=g_\theta(u_t,x)$의 reparameterization trick를 적용하면 다음 Algorithm 2를 진행할 수 있게 됩니다.

논문 내 Algorithm 2
Example: bivariate Gaussian
논문에서 중간에 예시로 제시한 것은 bivariate Gaussian 분포에 대한 학습 과정입니다.
우선 Gibbs sampling, 여러 변수에 대해서 차례로 샘플링을 진행하는 것을 방법 중 하나로 제시했습니다. 논문에서는 해당 깁스 샘플링의 식을 $p(z^i|z^{-i})=N(\mu_i,\sigma^2_i)$로 나타냈습니다. 간단히 설명하면 좌표 $(x, y)$에서 $x, y$값을 바탕으로 새로운 $x’$를 얻고, $x’$와 $y$를 바탕으로 새로운 $y’$를 얻는 형태이고 이때 정규분포를 활용해서 새로운 값을 만들어내게 됩니다.
다른 샘플링으로는 Over-relaxation method를 제시했고, 논문에서는 $z^i$를 $q(z_t^i|z_{t-1})=N[\mu_i+\alpha(z^i_{t-1}-\mu_i),\sigma_i^2(1-\alpha^2)]$로 연산한다고 표시하였습니다. 이 때 $\alpha$ 값은 수렴(mixing)을 더 빠르게 하는 용도로, 가속도와 유사한 개념으로 이전의 값을 얼마나 다시 활용하는지를 정할 -1에서 1 사이의 값입니다. 이 때 $\alpha=0$인 경우 이 방법이 깁스 샘플링과 완전히 동일해집니다.
논문에서는 추정하기로는 실험치인 $\alpha=-0.76$을 활용했을 때 over-relaxation method가 깁스 샘플링에 비해 상당히 빠르게 수렴하는 형태를 보여주었다고 합니다.
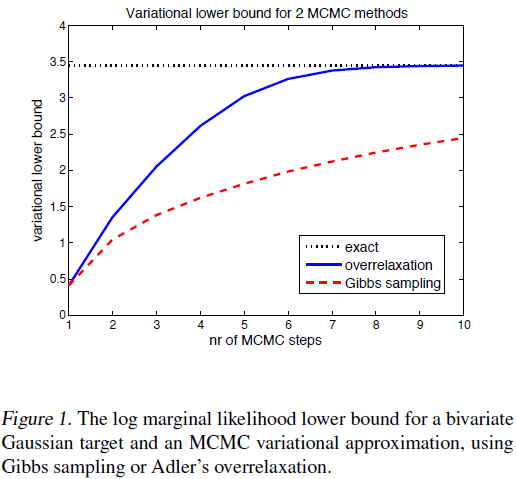
논문 내 Figure 1
추정하기로는 이 부분은 아래부터 설명할 Hamiltonian VI를 활용한 것에 대한 근거로, 이전의 상태를 추가로 반영하는 일종의 가속도 개념을 가져온 Over-relaxation method가 단순한 Gibbs Sampling보다 좋은 성능을 나타낸 것을 보여주기 위한 부분이라고 생각됩니다.
Hamiltonian VI
MCMC 중에서 Hamiltonian MC가 널리 사용되고 있음에 착안해서, MCMC와 VI를 섞은 구현체에서 해당 방법을 사용하기로 했고, 그 이름을 Hamiltonian VI로 정했다고 합니다.
우선 해당 내용을 시작하기 전,
Hamiltonian Dynamics
해밀턴 역학에 대해 간단히 설명드리겠습니다.
해밀턴 역학은 위치 벡터 $x$와 운동량 벡터 $p$를 활용해, 전체 에너지 $H$를 운동 에너지 $K$와 위치 에너지 $U$의 합으로 나타내는 역학입니다. 이를 식으로 나타내면 $H(x,p) = K(p) + U(x)$가 됩니다. 해당 식에서 시간 $t$를 활용해서 미분을 하면 $\frac{dx}{dt} = \frac{dH}{dp} = \frac{dK}{dp}$나 $\frac{dp}{dt} = -\frac{dH}{dx} = -\frac{dU}{dx}$ 등의 식을 얻을 수 있습니다.
이 해밀턴 역학은 단순한 역학으로 고등학교 물리 교과과정에서 배우며, 이 이론만으로 중력이 있는 상태에서의 포물선 운동이나 인공위성이 지구 주변의 일정한 궤도를 도는 궤도 운동 등을 설명할 수 있습니다.
Momentum
위 해밀턴 역학을 바탕으로 MCMC에 운동량(Momentum) 개념을 도입하기로 했습니다. 현재 위치값 $x$에서 운동량 $p$를 만들어 내고, 이 $(x, p)$ 값을 활용해서 새로운 $(x’, p’)$를 구해낸 다음 다시 위치값만 가져오는 식으로 동작하게 됩니다. 이렇게 동작한다면 전체 공간을 효율적으로 탐색할 수 있다고 저자들은 주장합니다.
개인적으로는 이러한 부분이 공전 궤도에 수렴하는 것과 비슷하게 실제 값을 멀 때는 빠르게, 가까울 때는 속도를 줄여 찾아나가는 것과 비슷하다는 느낌으로 이해했습니다.
Hamiltonian VI
그래서 이를 바탕으로 HVI 알고리즘을 만들었고, 그 내용은 아래와 같습니다.

논문 내 Algorithm 3
Experiment

논문 내 성능 비교
논문 내에서는 기존의 다른 논문과 비교했습니다. 이 때 SOTA인 DRAW 논문의 80.97과 비교해서 HVI가 최적의 경우에 81.94로, VI인 것을 감안했을 때 유사한 성능을 보이는 것으로도 우수한 성능을 보여주었다고 생각합니다. 개인적인 생각으로는 연산 시간의 차이도 같이 보여주었으면 비교가 용이했을 것 같은데 이 부분은 아쉽게 생각합니다.
Leapfrog step
논문의 실험 내용에서 Leapfrog step를 언급하고 있는데, 이는 해밀턴 역학에 사용되는 용어로 작은 stepsize를 두고 그 배수가 되는 시간에 상태를 측정하는 형태를 지니고 있다고 합니다. 논문의 figure 2는 leapfrog step를 진행함에 따라 exact와 유사한 모양을 보여주고 있으며, 이는 leapfrog step를 진행할수록 모델의 표현력이 증가하는, VI보다는 MCMC에 가까운 모양을 나타낸다고 생각합니다. 해당 leapfrog step와 관련해서는 Handbook of Markov Chain Monte Carlo라는 책에 제시된 내용을 확인해보시면 좋을 것 같습니다.
더불어 역학적인 측면에서 보자면,
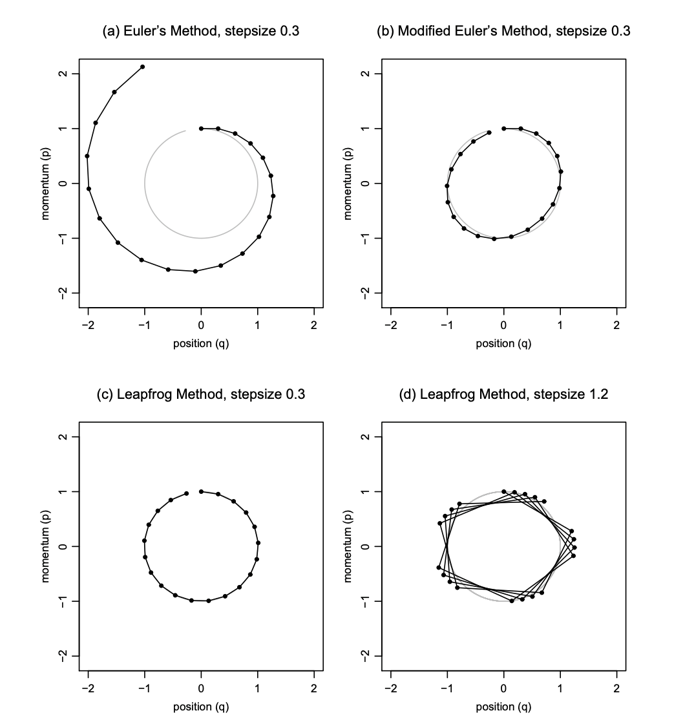
출처: Radford Neal, MCMC using Hamiltonian dynamics
위의 euler method와 비교해서 아래의 leapfrog method를 보면 stepsize가 크더라도 궤도에서 벗어나지 않도록 비교적 잘 유지되는 모습을 보이는 것 같습니다.
Conclusion
결론적으로 본 논문은 MCMC에 VI를 통합시키는 방법론을 제시했으며, 이를 실제로 구현한 Hamiltonian VI를 개발하였습니다. 더불어 이 HVI가 기존의 SOTA와 비교해서 더 빠른 시간에 유사한 정확도를 보여주고 있습니다. 더불어 이 HVI는 다른 논문에서 SOTA로 비교 대상으로 제시되고 있습니다.
본 논문에서는 위에 언급하지 않은 몇가지 추가적인 제안을 하였으며, 이는 다른 Variational Inference for Monte Carlo Objectivies와 같은 MCMC와 관련된 논문들에 활용되고 있음을 확인했습니다.
Subscribe via RSS
